|
|
 |
Exemplo 1
Nível Abaixo do Básico
Compõe a descrição do ponto 200 da Escala de Matemática – SARESP
H43 Associar informações apresentadas em listas e/ou tabelas simples aos gráficos que as representam e vice-versa.
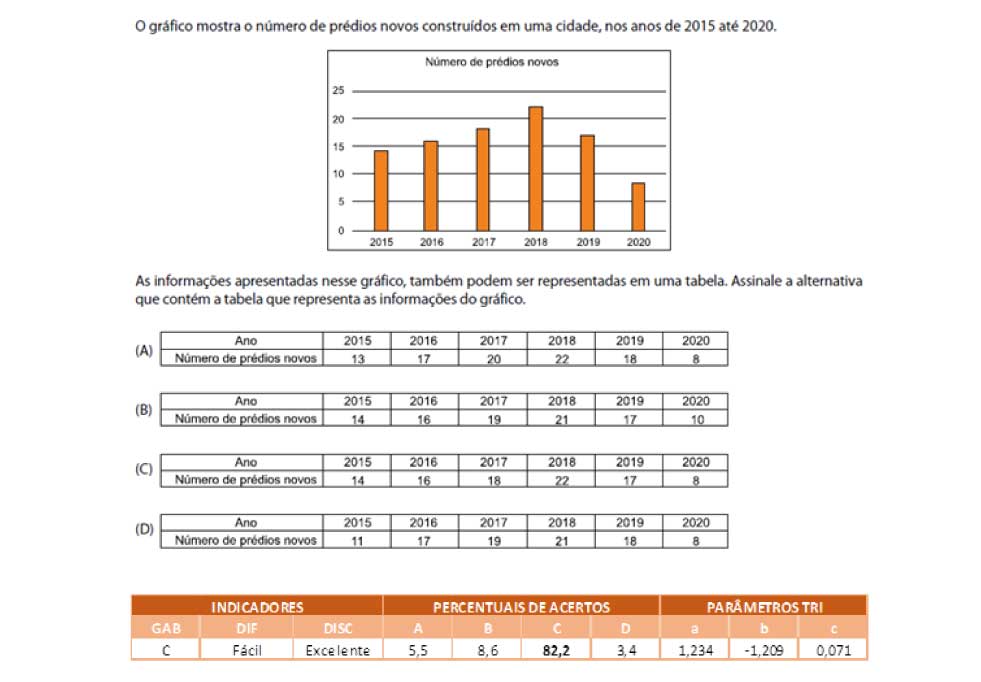
O item apresentado aborda a habilidade de associar as informações presentes em um gráfico de colunas a uma tabela simples. A obtenção da resposta depende da leitura correta dos dados apresentados no gráfico, sendo que:
- no ano de 2015 foram construídos menos de 15 prédios novos;
- no ano de 2016 esse número foi um pouco maior do que 15;
- no ano de 2017 se aproximou ainda mais de 20;
- no ano de 2018 superou 20, sendo o maior valor registrado no gráfico;
- no ano de 2019 o número de prédios construídos ficou entre o número observado em 2016 e 2017;
- no ano de 2020, menos de 10 prédios foram construídos.
Baseado nessas informações, conclui-se que a resposta correta é a alternativa (C). Esse item foi respondido corretamente por aproximadamente 82% dos estudantes, sendo considerado um item fácil e que apresentada excelente índice de discriminação para diferenciar o desempenho dos estudantes do grupo de Maior e de Menor Desempenho na prova.
Importante destacar que o distrator (B) foi apontado por quase 9% dos respondentes tem valores apresentados na tabela muito próximos da alternativa correta, ainda mais se considerarmos que as colunas estão posicionadas entre as linhas de grade de apoio do gráfico. Ainda sobre essa alternativa de resposta, cabe ressaltar que apenas o dado de 2020 apresenta um número não condizente com a leitura do gráfico. Assim sendo, é provável que os estudantes que optaram por essa resposta consigam fazer a associação, porém precisam de um refinamento em algumas situações que envolvem um conjunto maior de dados.
O processo inverso, ou seja, a partir de uma tabela obter o gráfico de colunas ou de barras também apresentou alto índice de acerto, reafirmando o bom desempenho nesse tipo de tarefa. Esse bom desempenho sofre pequena queda quando os dados se referem a tabelas com mais de uma entrada, principalmente nos grupos Intermediário e de Menor Desempenho. Inclusive, há de se destacar a necessidade de os estudantes melhorarem a leitura e a interpretação do comando da questão, uma vez que foi observado que para tabelas com mais de uma entrada, por vezes, apontam como alternativa correta um gráfico que apresenta os dados de uma entrada diferente daquela solicitada. Por exemplo, uma tabela que a apresentava dados de vacinação em alguns estados, continha as seguintes informações:
- Número de doses disponibilizadas
- % de pessoas vacinadas
- População total
Para esse item o comando era identificar o gráfico que representava corretamente o número de doses disponibilizadas. Mesmo assim, 28% dos respondentes indicaram como resposta um gráfico que trazia os números presentes na coluna do % de pessoas vacinadas. Ou seja, esses estudantes souberam reconhecer dados da tabela num gráfico, porém não os dados solicitados.
Por outro lado, resultados não tão bons são constatados quando a tarefa propõe a associação entre um gráfico de setores com valores em porcentagem e uma tabela com valores absolutos. Esse tipo de tarefa exige mais do que a simples transposição dos dados de uma tabela para um gráfico, pois requer que o estudante transforme aqueles números absolutos em parte de um todo, uma vez que o gráfico de setores possui essa característica associada a ideia de frequência relativa.
Frente a isso, cabe exemplificar uma situação observada ao longo da prova, em que o gráfico abaixo estava presente, observe:
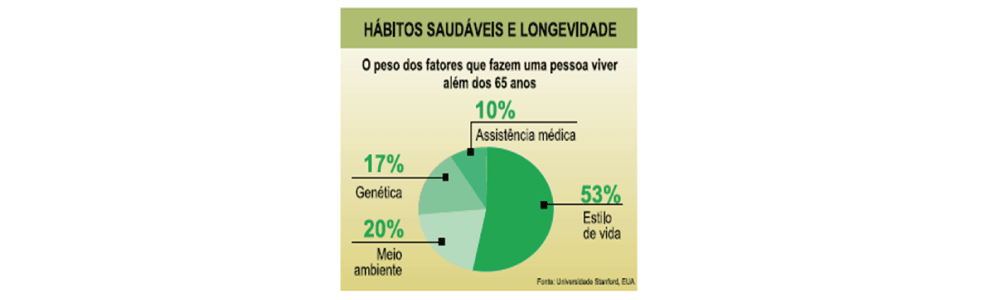
No item que trazia esse gráfico, todas as alternativas continham tabelas com os números 30, 51, 60 e 159, cabendo ao respondente identificar a entrada associada a cada um desses números. Nesse caso, pouco menos de dois terços do alunado foi capaz de relacionar 30 a assistência médica, 51 a genética, 60 ao meio ambiente e 159 ao estilo de vida. Ou seja, para pouco mais de um terço parece não haver relação direta entre a maior porcentagem e o maior número, ou seja, não percebem que a maior “fatia” do gráfico de setores é reflexo do maior número associado àquela entrada.
Curiosamente, quando o gráfico de setores não traz o percentual associado a cada setor, fazendo com que o estudante tenha que se apoiar somente nas características visuais do gráfico, o índice de acerto aumento. Isso sugere que há algum ruído quando o percentual aparece no gráfico, fazendo com que parte dos estudantes deixe de analisar a divisão do gráfico e passe a tentar fazer algum tipo de cálculo com a porcentagem apresentada.
|
 |
Exemplo 2
Nível Básico
Compõe a descrição do ponto 250 da Escala de Matemática – SARESP
H10 Efetuar cálculos que envolvam operações com números racionais (adição, subtração, multiplicação, divisão, potenciação - expoentes inteiros e radiciação).
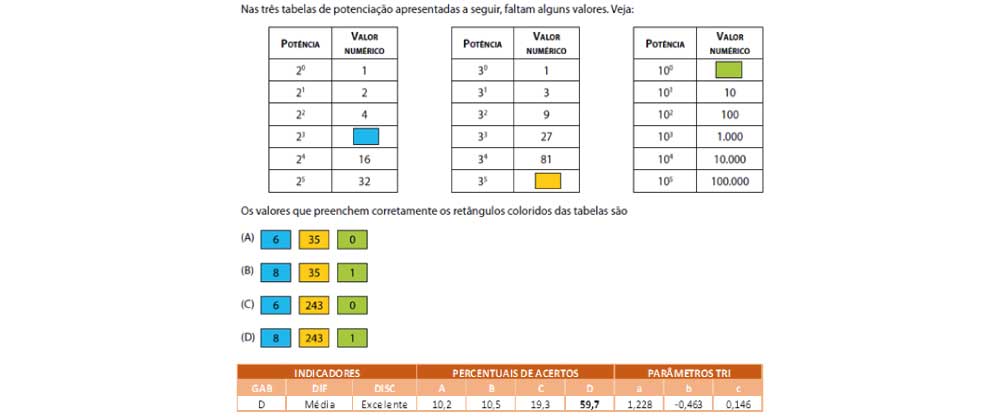
O item apresentado está associado a habilidade de calcular o resultado de uma potência. Nesse caso, espera-se que os estudantes sejam capazes de analisar as propriedades das três tabelas para então obter os números faltantes em cada uma delas, sendo que em todos os espaços a serem completados era solicitado o resultado da potência.
Ao analisar a distribuição das respostas dos estudantes observa-se que pouco mais de 20% deles se distribuíram nas alternativas (A) e (B), não percebendo que 35 resulta obrigatoriamente em um número maior do que 81, que é o resultado de 34. Numa linha semelhante, tem-se que aproximadamente 30% dos candidatos optaram pelas alternativas (A) ou (C) indicando que o resultado de 100 é igual a zero, não observando que nas outras tabelas tanto 20 como 30 resultam em 1. Ou seja, para esses estudantes que optaram pelas alternativas (A), (B) ou (C), o conjunto de informações das três tabelas não os permitiu perceber tais particularidades da potenciação.
O item foi corretamente respondido por aproximadamente 3 em cada 5 estudantes que o solucionaram. Estes foram capazes de observar as características presentes em cada uma das tabelas e associá-las ao conceito de potenciação, obtendo o resultado correto para cada uma das potências propostas. Porém, quando analisamos os resultados nos grupos de desempenho observamos que no de Menor Desempenho o índice de acerto cai para aproximadamente 35%, mostrando que esse grupo precisa ser alvo de uma ação do professorado em busca de melhorar esse índice de aproveitamento.
Apesar de a tarefa envolver o cálculo de 3 potências, esse item foi mais acertado do que outro presente na prova que perguntava apenas o valor de 32. Para esse segundo caso, a grande maioria dos respondentes se dividiram entre 32 ser igual a 6 (incorreto – provável resultado de 3x2) ou 9 (correto – uso da definição, já que 32 = 3x3 = 9), fazendo com que o índice de acerto fosse inferior a 50%. Se olharmos novamente para o Grupo de Menor Desempenho, 55% destes optaram por 6 como sendo o resultado dessa potenciação, enquanto que no Grupo de Maior Desempenho esse percentual é de 16,3%.
A ideia de potenciação acaba por impactar diretamente em outros conceitos e habilidades da matemática, explorados ao longo da prova. Em relação a isso, foram observadas dificuldades relacionadas as seguintes tarefas:
- Identificar a solução de uma equação quadrática: casos em que o item formulado permite o teste das alternativas de resposta, observou-se que é frequente o emprego de
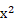 como sendo como sendo 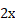 . Por exemplo, para a equação . Por exemplo, para a equação 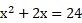 tivemos x = 6 como principal alternativa de resposta assinalada, o que sugere, possivelmente que os respondentes fizeram tivemos x = 6 como principal alternativa de resposta assinalada, o que sugere, possivelmente que os respondentes fizeram 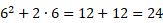 . .
- Desenvolver expressões algébricas, em particular o trinômio do quadrado perfeito: nesse caso, nota-se que ao fazer, por exemplo,
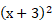 boa parte dos estudantes não associa essa expressão com boa parte dos estudantes não associa essa expressão com 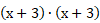 , deixando de fazer a distributiva e trazendo como resposta , deixando de fazer a distributiva e trazendo como resposta 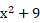 ou até mesmo ou até mesmo 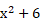 . .
- Reconhecer a escrita de um número em notação científica: muitas vezes se observa a escolha de certas alternativas de resposta que sugerem o emprego de determinadas técnicas que não apresentam sustentação matemática e não respeitam as propriedades de potenciação. Por exemplo, a escrita do número 0,008 em notação científica está relacionada, para mais da metade dos estudantes que realizaram o teste, com a potência 10–2, muito provavelmente por associarem essa potência com o número de zeros a direita da vírgula. Destaca-se que essa ideia é uma estratégia não condizente com as propriedades de potenciação.
Por fim, vale lembrar uma vez mais que, no comparativo de desempenho da edição 2021 com edições anteriores, o cálculo de potências foi uma das tarefas em que foi observado maior queda nos índices de acerto de itens comuns, de modo que a acentuação da dificuldade nessa temática é um dos motivos para a queda na proficiência média turma do 9º ano EF.
|
 |
Exemplo 3
Nível Adequado
Compõe a descrição do ponto 325 da Escala de Matemática – SARESP
H01 Reconhecer as diferentes representações de um número racional.

O item apresentado envolve o conceito de razão (comparação) entre o número de arremessos certos e o número total de arremessos feitos por um jogador de basquete. Nesse caso, a razão é dada pela fração  , que ao ser simplificada resulta na fração , que ao ser simplificada resulta na fração  (alternativa D), resposta essa dada por quase um terço dos estudantes, caracterizando-a como uma questão como difícil. Mesmo se considerarmos apenas o Grupo de Maior Desempenho o índice de acerto ficou em aproximadamente 56%, mostrando que para esses estudantes o conceito também requer refinamento junto ao professorado. (alternativa D), resposta essa dada por quase um terço dos estudantes, caracterizando-a como uma questão como difícil. Mesmo se considerarmos apenas o Grupo de Maior Desempenho o índice de acerto ficou em aproximadamente 56%, mostrando que para esses estudantes o conceito também requer refinamento junto ao professorado.
Ao fazer a análise do erro, observa-se um fato alarmante: quase metade dos respondentes assinalou as opções (A) ou (C) como resposta, indicando uma fração maior do que 1. Isso mostra que esses estudantes não estão sabendo interpretar a razão solicitada, que representa o aproveitamento do jogador, sendo que esta varia sempre de 0 a 1. Ao indicar o aproveitamento como sendo uma fração maior do que 1, afirma-se que o jogador acertou mais arremessos do que o total realizado, o que é incoerente com o significado da razão solicitada. Em complemento, temos pouco mais de 18% dos respondentes apontando a fração  como sendo uma simplificação da razão como sendo uma simplificação da razão  , apesar dessas frações não serem equivalentes. , apesar dessas frações não serem equivalentes.
Cabe destacar que o conceito de frações equivalentes está muito relacionado ao conceito de proporção, de modo que ao resolver problemas envolvendo grandezas diretamente proporcionais, a ideia que sustenta o emprego da regra de três é exatamente o de frações equivalentes. Nos itens que abordavam relações de proporcionalidade direta, chama a atenção o fato de que:
- Quase 80% dos estudantes calcularam corretamente a quantidade de água desperdiçada em um vazamento ao longo de um dia, dada a quantidade de água desperdiçada por hora. Consideraram-se apenas o Grupo de Menor Desempenho esse índice de acerto se reduz para aproximadamente 52%.
- Praticamente 60% dos estudantes conseguiram mobilizar seu conhecimento para resolver um problema no qual era necessário determinar a quantidade de peças produzidas por minuto por uma máquina específica, dado que ela conseguia fabricar 5 peças a cada 6 segundos. Apesar de exigir uma comparação entre unidades de tempo, como no caso anterior, o índice de acerto foi menor que o aferido no primeiro caso.
- 57,5% dos respondentes conseguiram resolver problema envolvendo a determinação do número de carros que transitam num determinado lugar, dado que, em média, transitam 27 carros por minuto nesse local.
- Quase 53% dos estudantes calcularam o número correto de árvores preservadas ao se reciclar uma tonelada de papel, dada a quantidade de árvores não cortadas para cada 100 quilos de papel reciclado.
- Apenas 40% dos respondentes souberam determinar corretamente o preço a ser pago na compra de 350 g de certo produto, dado o valor cobrado por 100 g do mesmo. (situação relativamente comum em supermercados, varejões, mercearias e feiras)
- Pouco mais de um terço dos estudantes (37%) conseguiram calcular corretamente a quantidade de adubo, em gramas, a ser administrado em um canteiro retangular, dado que cada metro quadrado do canteiro deve receber 50 g de adubo.
- Menos de 28% dos estudantes foram capazes de converter uma medida dada em pés para palmos, dado que 2 pés equivalem a 3 palmos. A alternativa mais assinalada (36,1%) indicou que os estudantes consideraram que para converter qualquer medida em pés para palmos basta subtrair uma unidade no número apresentado.
As situações apresentadas anteriormente foram organizadas a partir do índice de acerto aferido em cada uma delas, de modo decrescente, visando mostrar elementos para o professorado poder identificar o que tem sido mais bem assimilado pelos estudantes da rede estadual.
Em complemento a ideia de razão, frações equivalentes e grandezas proporcionais, têm-se as diferentes escritas de um número racional. A partir dos itens propostos nesse SARESP 2021, observou-se que:
- Cerca de 84% dos respondentes não foram capazes de associar uma fração imprópria a uma fração mista equivalente.
- Pouco mais de 70% dos estudantes entende que a representação fracionária e decimal de um número deve ser composta dos mesmos algarismos. Por exemplo, esses estudantes entendem que a representação decimal da fração
 é o número 3,5. é o número 3,5.
- Quase 20% dos respondentes indicou que há os números decimais 1,25 e 5,4 são maneiras diferentes de representar a fração
 . Ou seja, para esses estudantes, o conceito de equivalência permite dizer que 1,25 e 5,4 são números equivalentes. . Ou seja, para esses estudantes, o conceito de equivalência permite dizer que 1,25 e 5,4 são números equivalentes.
Por fim, destaca-se que parte das considerações feitas para esse exemplo já tinham sido expostas em relatórios anteriores, no entanto, foi percebido um aumento no percentual de estudantes cometendo tais erros nessa última edição.
|
 |
Exemplo 4
Nível Avançado
Compõe a descrição do ponto 375 da Escala de Matemática – SARESP
H35 Aplicar o Teorema de Tales como uma forma de ocorrência da ideia de proporcionalidade, em diferentes contextos.
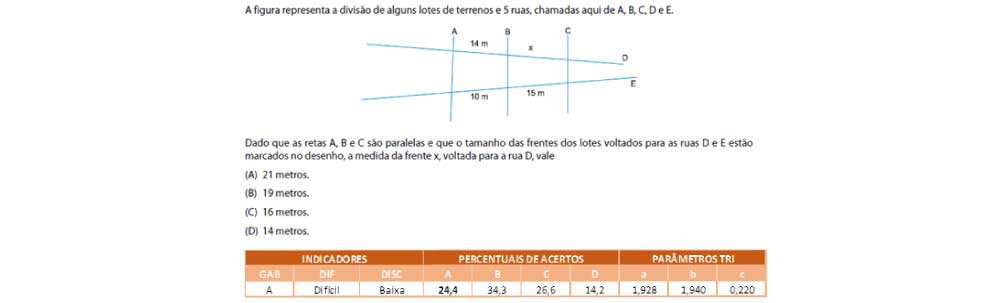
O item apresentado está relacionado a habilidade de resolver problema envolvendo o teorema de Tales. A situação apresentada traz uma contextualização muito recorrente para a temática, amplamente utilizada em vários materiais didáticos. A solução perpassa pela percepção de que o modelo matemático apresentado permite o uso do teorema de Tales, uma vez que as ruas D e E são interceptadas por outras três paralelas. Nesse caso, a solução é obtida a partir da seguinte relação:
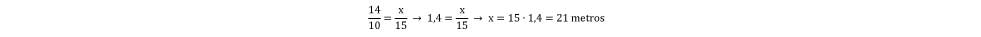
A alternativa correta (A) foi assinalada por aproximadamente um quarto dos estudantes, caracterizando o item como difícil para o grupo de respondentes. A alternativa mais assinalada foi (B), possivelmente obtida a partir de uma ideia associada a operação adição. Nesse caso, entende-se que os estudantes podem ter lançado mão do seguinte raciocínio:

Essa estratégia mostra que respondente muito provavelmente não relacionou a situação com o Teorema de Tales, ou mesmo não compreendeu a ideia deste teorema. Outro dado que reforça a desconexão dessa situação-problema com o teorema de Tales é que praticamente 40% dos respondentes optaram pelas respostas 16 ou 14 metros, sendo ambas muito possivelmente feitas a partir de impressões visuais para determinação da medida indicada por x. Ou seja, os estudantes provavelmente fizeram uma comparação das outras medidas presentes na imagem.
Esses dois tipos de estratégias também puderam ser observados na resolução de outro item envolvendo a mesma habilidade, o que reforça que essas resoluções caracterizam erros comuns a serem considerados e corrigidos nas aulas pelo professorado.
Cabe destacar que num outro item dessa temática foi apresentado o seguinte esquema:

O objetivo da questão era determinar as medidas de x e y. Pouco mais de um terço dos respondentes apontou que 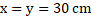 ou que o valor de x é maior que o de y. Isso mostra que esses estudantes não perceberam que o fato de o lado que mede 22 ser maior que o lado que mede 18, implica em a medida y, lado oposto ao que mede 22, ser obrigatoriamente maior do que a medida x, lado oposto ao que mede 18. ou que o valor de x é maior que o de y. Isso mostra que esses estudantes não perceberam que o fato de o lado que mede 22 ser maior que o lado que mede 18, implica em a medida y, lado oposto ao que mede 22, ser obrigatoriamente maior do que a medida x, lado oposto ao que mede 18.
Em complemento as observações feitas para o Teorema de Tales, é importante destacar o desempenho dos estudantes em problemas relacionados a outro teorema importante da geometria, o de Pitágoras. Nos casos associados a esse outro teorema, a análise do desempenho dos estudantes mostrou dois erros recorrentes. São eles:
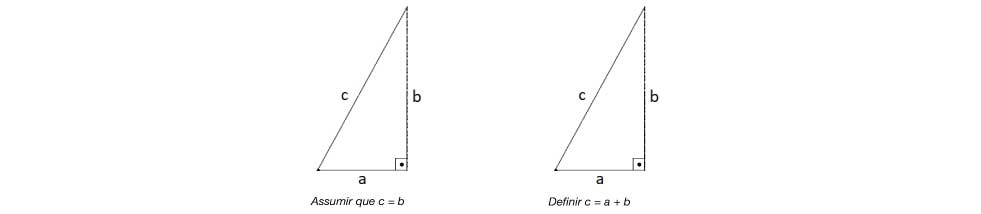
Por fim, reitera-se a necessidade de um olhar próximo do professorado para as dificuldades que os estudantes estão trazendo nessa retomada de ensino presencial. Muitas delas exigirão um recomeçar e um ressignificar ideias que já haviam sido superadas em anos anteriores por boa parte dos estudantes. Ou seja, mais do que relembrar conquistas anteriores, será necessário conquista-las uma vez mais.
|
|
|
|

|
