|
|
 |
Nessa edição de 2021 da prova SARESP para o 2º ano do Ensino Fundamental foram utilizadas questões objetivas pela primeira vez, o que precisa ser levado em consideração na análise dos resultados. Trata-se de um modelo novo de prova para esse ano, em um formato que pode ser desafiador aos estudantes nesse primeiro contato. Assim, não é viável estabelecer uma comparação entre o resultado dessa edição com edições anteriores. A prova do 2º ano contou com 70 questões de múltipla escolha e 2 questões de respostas construídas para a montagem dos cadernos de prova.
Outro fator importante que precisa ser considerado na análise dos resultados, que teve profundo impacto nas condições de aprendizagem das crianças, foi a pandemia Covid-19. Desde 2020, devido a necessidade do distanciamento social imposta pela pandemia, a dinâmica escolar precisou ser repensada e apresentou diversos desafios aos profissionais da educação, aos estudantes e seus familiares. Vale destacar, sobretudo, que especificamente esses estudantes do 2º ano frequentaram o Ensino Fundamental presencialmente por pouquíssimo tempo – assim que começaram a conhecer a nova rotina escolar no 1º ano, ocorreu a interrupção das aulas presenciais.
Diante das incertezas desse novo cenário tão atípico, propostas de ensino remoto e interações virtuais passaram a ser a nova realidade das escolas nesse período e os professores precisaram descobrir novos meios de promover a aprendizagem dos seus estudantes, contando ainda mais com a parceria das famílias.
Em relação ao ensino da Matemática nos Anos Iniciais, sabemos da importância da mediação dos professores e das práticas de sala de aula para a aprendizagem que envolvem o uso de materiais manipulativos, proposições de situações concretas, vivências de jogos, entre outras possibilidades, que acabaram sendo inviabilizadas durante o período pandêmico.
Os desafios foram muitos: incerteza de quanto tempo o distanciamento seria necessário para a preservação da vida, adaptação ao novo contexto, dificuldades materiais e tecnológicas, como falta de aparelhos adequados para que os estudantes pudessem acompanhar as aulas, problemas de conexão de internet, entre outras tantas questões específicas a cada região do estado de São Paulo.
Todo esse panorama ressalta a importância de uma avaliação sistematizada como o SARESP, que possibilita mais um olhar diagnóstico da aprendizagem, trazendo informações importantes a serem refletidas pela comunidade escolar. Tais reflexões podem contribuir para o planejamento de ações futuras, visando fortalecer o ensino e focalizar problemáticas a serem sanadas.
PARTE 1 – ITENS DE RESPOSTA CONSTRUÍDA
Conforme apontado anteriormente, a prova do 2º ano contou com 20 questões de múltipla escolha e 2 questões de respostas construídas.
A prova do 2º ano EF também contou com a aplicação de questões de respostas construídas, sendo a correção destas feita apenas com um grupo amostral. A seguir apresentaremos as questões, os critérios de correção e faremos uma breve discussão a respeito dos objetivos de cada uma delas. Há duas versões de cada questão, de acordo com o período.
Foram propostas duas questões de resposta construída para os estudantes do 2º ano.
A primeira questão apresenta ao estudante cinco números, sendo quatro da ordem da dezena e um da ordem da centena. A criança deveria ordenar esses cinco números de maneira crescente, sendo que o enunciado explicita que essa organização é do menor para o maior.
O objetivo é observar as relações que o estudante estabelece entre esses números, se leva em consideração a maior ordem do número para determinar a sequência. Por exemplo, é comum crianças que ainda estão se apropriando do Sistema Decimal de Numeração indicar o 29 como um número maior do que o 31, por considerar o algarismo da unidade (9 e 1), em vez do algarismo da dezena (2 e 3). Outro conhecimento importante que é possível observar nessa questão é se o estudante percebe que o único número da ordem das centenas é o maior de todos os números apresentados, uma vez que tem uma ordem a mais do que o restante.
Além disso, é comum as crianças dos Anos Iniciais, ao se depararem com ordenamento de números, se preocuparem apenas com as pontas: determinam o menor, determinam o maior, mas se perdem na organização dos números intermediários.
Veja a questão a seguir e seus critérios para correção:
Versão Manhã:
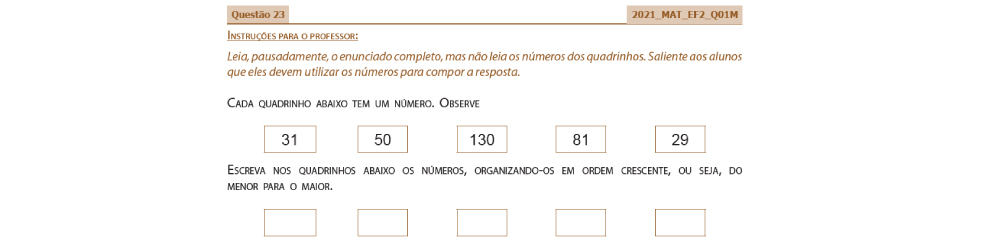
Critérios de correção:

Observação: caso o estudante cometa apenas UM ERRO de transcrição, selecionar o critério correspondente. Quando houver mais de um erro de transcrição, automaticamente, a resposta entra no critério F (Outras respostas que não as assinaladas em (A), (B), (C), (D) ou (E)).
Versão Tarde:

Critérios de correção:

Observação: caso o estudante cometa apenas UM ERRO de transcrição, selecionar o critério correspondente, mais de um erro de transcrição automaticamente cai no critério F.
A segunda questão de resposta construída apresentada aos estudantes do 2º ano possuía duas partes. A primeira consistia em uma adição, na qual a primeira parcela e o resultado estão dados, cabendo ao estudante determinar a segunda parcela para que o cálculo fique correto. Para descobrir essa parcela, os estudantes poderiam calcular mentalmente, fazer desenhos, contas, estimar e conferir suas respostas.
Uma das estratégias possíveis seria a criança contar quanto falta para o 28 chegar ao 37 (ou o 38 chegar no 47 na versão da tarde), se apoiando ou não no registro pictórico. Outra possibilidade seria perceber que 28 mais 10 resultaria em 38 e por isso a resposta é um a menos que 10, ou seja, 9.
Alguns estudantes podem ter optado pelo cálculo inverso, ou seja, fazer 37 menos 28 (ou 47 menos 38 na versão da tarde). Um erro comum nesse caso, é a criança subtrair na ordem das unidades o maior algarismo do menor, em vez de fazer o empréstimo necessário (faz 8 menos 7, em vez de 7 menos 8), errando o cálculo. Nesse mesmo caso, pode ocorrer da criança fazer o empréstimo para a unidade, mas esquecer de retirar a dezena que foi emprestada e achar um resultado com uma dezena a mais.
Já na segunda parte da questão, foi apresentada uma subtração com o minuendo e a diferença determinados, cabendo ao estudante responder qual o subtraendo para que o cálculo ficasse correto. A criança precisava perceber que no resultado a dezena se mantinha o mesmo do número inicial e, por isso, deveria retirar apenas da ordem das unidades.
As estratégias possíveis também eram variadas nesse caso. Os estudantes poderiam contar quanto precisavam tirar do 16 para sobrar 10 (ou do 26 para sobrar 20 na versão da tarde), fazer registro pictórico, estimar e conferir a resposta.
Caso o estudante optasse por fazer um cálculo com algoritmo, precisaria compreender que nesse caso não se trata da operação inversa como na adição e sim uma subtração, na qual deveria retirar do resultado o primeiro número apresentado (16 – 10 ou 26 – 20).
Mesmo que a criança tenha errado, é preciso observar se pelo menos indicou como resposta um número menor do que o minuendo, princípio importante dos cálculos de subtração com números naturais.
Veja a seguir a questão e seus critérios de correção:
Versão Manhã:

Critérios de correção:
PARTE A

Critérios de correção:
PARTE B

Versão Tarde:

Critérios de correção:
PARTE A

Critérios de correção:
PARTE B

PARTE 2 – ITENS DE MÚLTIPLA ESCOLHA
A Matriz de Referência para o SARESP traz um conjunto de habilidades que servem para nortear a montagem das provas do 5ºEF, 9ºEF e 3ªEM. Contudo, esse documento oficial, que data de 2009, não apresenta um conjunto de habilidades para os anos iniciais do Ensino Fundamental.
Em vista disso, ao longo dos anos, as provas do 2ºEF e 3ºEF foram sendo construídas com base no Currículo Paulista, consolidando um rol de habilidades recorrentes na elaboração dessas provas. Na edição de 2021, devido ao aumento do número de questões objetivas, esse rol precisou ser ampliado. Para tanto, foram privilegiadas as habilidades essenciais, uma vez que estas consideram as adequações pensadas pela Secretaria de Educação frente aos impactos escolares decorrentes da pandemia de Covid-19.
Em suma, os itens propostos utilizados na composição das provas do 2ºEF e 3ºEF do SARESP 2021 são baseados num histórico, que assegura melhor comparabilidade nos resultados de diferentes edições, e na realidade escolar da rede estadual, ao se nortear pelas habilidades do Currículo Paulista indicadas como essenciais pela SEDUC.
Nessa edição de 2021 da prova SARESP para o 2º ano do Ensino Fundamental foram utilizadas questões objetivas pela primeira vez, o que precisa ser levado em consideração na análise dos resultados. Trata-se de um modelo novo de prova para esse ano, em um formato que pode ser desafiador aos estudantes nesse primeiro contato. Assim, não é viável estabelecer uma comparação entre o resultado dessa edição com edições anteriores.
Outro fator importante que precisa ser considerado na análise dos resultados, que teve profundo impacto nas condições de aprendizagem das crianças, foi a pandemia Covid-19. Desde 2020, devido a necessidade do distanciamento social imposta pela pandemia, a dinâmica escolar precisou ser repensada e apresentou diversos desafios aos profissionais da educação, aos estudantes e seus familiares. Vale destacar, sobretudo, que especificamente esses estudantes do 2º ano frequentaram o Ensino Fundamental presencialmente por pouquíssimo tempo – assim que começaram a conhecer a nova rotina escolar no 1º ano, ocorreu a interrupção das aulas presenciais.
Diante das incertezas desse novo cenário tão atípico, propostas de ensino remoto e interações virtuais passaram a ser a nova realidade das escolas nesse período e os professores precisaram descobrir novos meios de promover a aprendizagem dos seus estudantes, contando ainda mais com a parceria das famílias.
Em relação ao ensino da Matemática nos Anos Iniciais, sabemos da importância da mediação dos professores e das práticas de sala de aula para a aprendizagem que envolvem o uso de materiais manipulativos, proposições de situações concretas, vivências de jogos, entre outras possibilidades, que acabaram sendo inviabilizadas durante o período pandêmico.
Os desafios foram muitos: incerteza de quanto tempo o distanciamento seria necessário para a preservação da vida, adaptação ao novo contexto, dificuldades materiais e tecnológicas, como falta de aparelhos adequados para que os estudantes pudessem acompanhar as aulas, problemas de conexão de internet, entre outras tantas questões específicas a cada região do estado de São Paulo.
Todo esse panorama ressalta a importância de uma avaliação sistematizada como o SARESP, que possibilita mais um olhar diagnóstico da aprendizagem, trazendo informações importantes a serem refletidas pela comunidade escolar. Tais reflexões podem contribuir para o planejamento de ações futuras, visando fortalecer o ensino e focalizar problemáticas a serem sanadas.
Considerando os resultados aferidos, de maneira geral, a distribuição dos estudantes do 2º ano nos níveis de proficiência ficou da seguinte maneira: 33% no nível insatisfatório, 44% no nível satisfatório e 23% acima do satisfatório. Como apontando anteriormente, não é possível traçar uma comparação desse resultado com anos anteriores. Mas podemos enfatizar que a somatória dos níveis satisfatório e acima do satisfatório abarcou quase 70% dos estudantes e ao se considerar o contexto pandêmico se revelou um bom resultado. Porém, os 33% de estudantes que ficaram no nível insatisfatório correspondem a um número significativo e merecem um olhar cuidadoso da comunidade escolar em relação a aprendizagem matemática.
A percepção dos estudantes, em relação ao grau de dificuldade dos itens, oscilou entre fácil e média e está destacada na tabela a seguir:
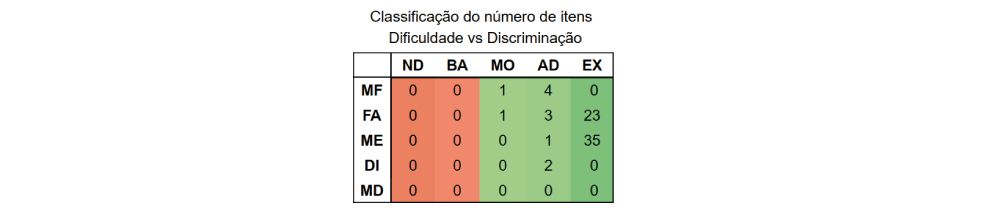
[Nota: Dificuldade: Muito Fácil (MF); Fácil (FA); Médio (ME); Difícil (DI) e Muito Difícil (MD) e Discriminação: Não Discrimina (ND); Baixa (BA); Moderada (MO) Adequada (AD) e Excelente (EX)]
De maneira geral, pode-se afirmar que os estudantes apresentaram facilidade principalmente em itens envolvendo contagem, comparação entre figuras geométricas e objetos do cotidiano, leitura de gráficos e tabelas em questões envolvendo preferências, reconhecimento do valor de cédulas e moedas e situações problemas aditivas.
A seguir, apresentamos quatro questões da prova para ilustrar o desempenho dos estudantes em itens ancorados em diferentes pontos da escala de proficiência. Atrelado a esses itens, tecemos observações gerais do desempenho dos estudantes na prova, principalmente para casos em que possíveis erros foram constatados, o que traz informações relevantes para reflexão e orientação de trabalho dos professores da rede estadual.

EXEMPLO 1
Nível Abaixo do Básico
Compõe a descrição do ponto 70 da Escala de Matemática – SARESP
(EF01MA13) Relacionar figuras geométricas espaciais (cones, cilindros, esferas e blocos retangulares) a objetos familiares do mundo físico.

O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Abaixo do Básico. A tarefa envolve reconhecer dentre diferentes borrachas aquela que se assemelha a um paralelepípedo (não cúbico) com apoio de imagem e sem a necessidade de nomear a forma geométrica. A criança precisava fazer a correspondência entre a representação da forma apresentada no enunciado e a mesma forma dentre as alternativas, sendo a correta apenas exposta em uma perspectiva diferente, o que pode se revelar um desafio para crianças pequenas.
Responderam corretamente esse item cerca de 80% dos estudantes. Os demais estudantes que responderam, se dividiram igualmente entre as três alternativas erradas (cerca de 1% para cada alternativa), não destacando nenhuma delas como possível erro comum.
Chama atenção o número significativo de crianças que não escolheu nenhuma das alternativas (quase 16%), abrindo espaço para questionamentos do porquê não realizaram a proposta. Esse comportamento não ocorreu, por exemplo, em outro item que abordava a mesma habilidade, porém com um cubo como referência no enunciado – cerca de 93% dos estudantes responderam corretamente e apenas 3,5% não optaram por nenhuma das alternativas, indicando possivelmente uma ênfase maior no trabalho com essa forma espacial.

EXEMPLO 2
Nível Básico
Compõe a descrição do ponto 150 da Escala de Matemática – SARESP
(EF02MA06) Resolver e elaborar problemas de adição e de subtração, envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar, utilizando estratégias pessoais ou convencionais.
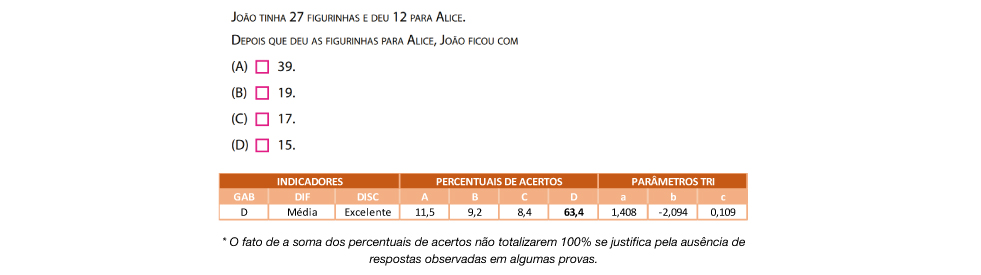
O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Básico. Trata da resolução de uma situação-problema envolvendo uma subtração (transformação) para determinar o número de figurinhas restantes de uma pessoa, dada a quantidade que ela tinha inicialmente e a quantidade que ela deu para outra pessoa.
Esse item caracteriza-se como nível básico pois propõe uma subtração (27 – 12 = 15) na qual não é necessário o uso do recurso, além de apresentar números apropriados para que a criança utilizasse registro pictórico como uma estratégia para solucionar o problema, caso desejasse.
Ao analisar o desempenho das crianças, destaca-se que a alternativa correta foi assinalada por 63,4% dos estudantes, pouco mais da metade. Cerca de 17% dos respondentes se dividiram entre as alternativas B (19) e C (17), revelando que, apesar de não terem acertado o resultado, possivelmente compreenderam que deveria ser feita uma subtração. Portanto, pode-se conjecturar que cerca de 80% dos estudantes compreenderam a situação proposta adequadamente e o cálculo que precisava ser feito, e quase um quarto desses, por algum motivo, não conseguiu chegar ao resultado esperado.
Chama a atenção os 11,5% de estudantes que responderam a alternativa A (39), ou seja, somaram os números presentes no enunciado, indicando que não compreenderam a situação proposta. Foi possível observar o mesmo comportamento em outros itens de resolução de problemas envolvendo subtrações, ou seja, uma porcentagem considerável de estudantes indicarem o resultado da soma como resposta. Tal situação merece um olhar investigativo dos professores sobre os possíveis motivos que levam esses estudantes a não interpretarem corretamente a situação proposta. É importante desde o 1º ano apresentar às crianças um repertório de diferentes situações-problema que envolvam as quatro operações básicas, de maneira que possam multiplicar, dividir, somar ou subtrair utilizando suas estratégias pessoais, evitando dar ênfase a um tipo em detrimento de outro.

EXEMPLO 3
Nível Adequado
Compõe a descrição do ponto 175 da Escala de Matemática – SARESP
(EF02MA22) Comparar informações de pesquisas apresentadas por meio de tabelas de dupla entrada e em gráficos de colunas simples ou barras, para melhor compreender aspectos da realidade próxima.
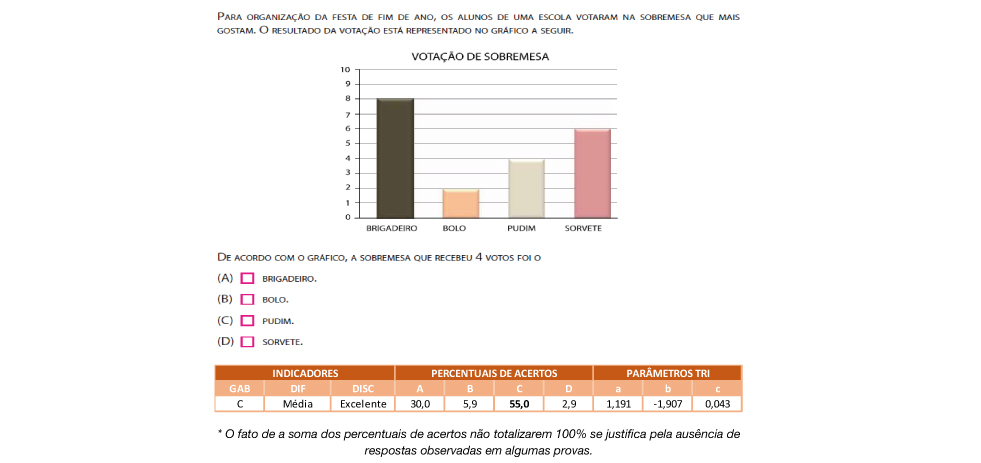
O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Adequada. Requer que o estudante identifique em um gráfico de colunas a entrada referente a 4 votos, sendo que esse número não reflete nem a maior nem a menor coluna.
Em relação ao desempenho nesse item, 55% dos estudantes identificaram corretamente a coluna que correspondia a 4 votos (pudim). É um indicativo importante 30% dos respondentes terem apontado a alternativa A (brigadeiro) como resposta, possivelmente por se tratar da maior coluna. A principal hipótese para essa porcentagem tão significativa refere-se ao tipo de exploração de gráficos que muitas vezes é feita com os estudantes, dando-se ênfase aos maiores índices, deixando em segundo plano outras leituras possíveis dos dados apresentados.
A análise de outros itens que também envolviam leitura de gráficos e tabelas, cuja pergunta relacionava-se ao menor índice ou dados empatados, revelou uma considerável porcentagem de estudantes que optou pela alternativa que indicava os maiores índices e não a resposta correta. Trata-se de uma observação importante, que revela a necessidade da ampliação das interpretações e discussões em sala de aula de gráficos e tabelas.
Ampliar o repertório do estudante, propondo diversas tarefas envolvendo diferentes tipos de gráficos e tabelas, é fundamental tanto para o desenvolvimento da habilidade de leitura e identificação de informações como para a habilidade de análise de dados. Essa segunda, mais complexa do que a primeira, só pode ser devidamente explorada se a criança for capaz de extrair de maneira clara e natural os dados compilados e apresentados nas tabelas e gráficos. Em suma, o desenvolvimento da habilidade de analisar só poderá ocorrer de modo pleno se os estudantes forem capazes de fazer a leitura correta dessas representações de coletâneas de dados.

EXEMPLO 4
Nível Avançado
Compõe a descrição do ponto 200 da Escala de Matemática – SARESP
(EF02MA21) Classificar resultados de eventos cotidianos aleatórios como “pouco prováveis”, “muito prováveis”, “improváveis” e “impossíveis”.
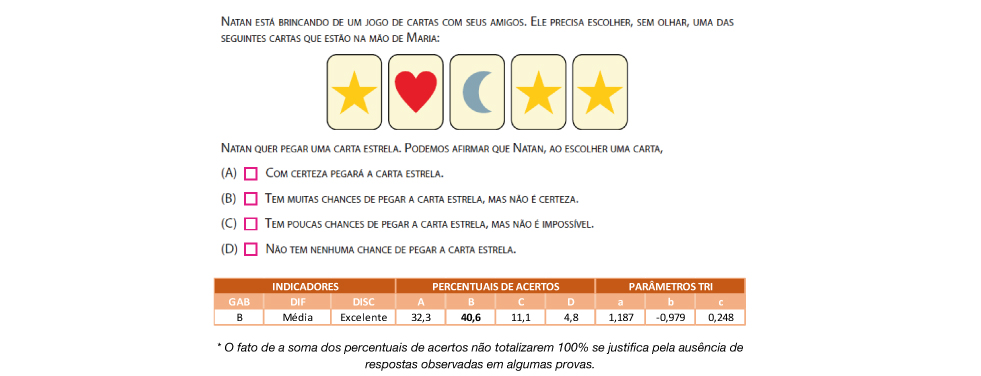
O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Avançada. O estudante precisava classificar como “tem muitas chances, mas não é certeza” a possibilidade de sortear determinada carta dentre cinco cartas, sendo que havia 3 cartas iguais a que se pretendia sortear.
Em relação ao desempenho nesse item, 40,6% dos estudantes indicaram a alternativa correta. A alternativa A (com certeza pegará a carta estrela) foi a segunda mais indicada, contando com 32,3% das respostas do alunado. Outros 11,1% indicaram que “tem poucas chances de pegar a carta estrela, mas não é impossível” e 4,8% indicaram como “não tem nenhuma chance de pegar a carta estrela”.
É compreensível um índice de 32,3% que responderam como certeza que Natan pegaria a carta, pois além de ser para a criança nessa idade muito tênue a diferença entre certeza e muita chance, envolve a expectativa de que o fato se concretize, uma vez que encaram essas propostas como um jogo.
Questões envolvendo probabilidade exigem certo nível de abstração dos estudantes, que precisa ser trabalhada nessa idade, pois requer que as crianças imaginem e compreendam todos os cenários possíveis. Por isso, é fundamental que os estudantes vivenciem concretamente situações como essa, coloquem “a prova” suas hipóteses e que essas sejam discutidas recorrentemente para que possam compreender a diferença entre um evento certo, um evento muito provável, um evento pouco provável e um impossível.
|
 |
|
|
|

|
