|
|
 |
Exemplo 1
Nível Abaixo do Básico
Compõe a descrição do ponto 150 da Escala de Matemática – SARESP
H02 Relacionar a escrita numérica às regras do sistema posicional de numeração.
O item apresentado aborda propriedades do sistema decimal de numeração, visando a capacidade do estudante de decompor um número formado por 4 algarismos diferentes de zero, em função de suas ordens. Essa tarefa, considerada muito fácil, foi acertada por 86% dos respondentes, sendo que esse índice sobe para 98,6% no Grupo de Maior Desempenho. Enquanto isso, no Grupo de Menor Desempenho, o índice de acerto se restringe a praticamente dois terços dos estudantes. Ainda nesse último grupo, cabe destacar que os distratores (A) e (C) foram a opção de escolha de quase 25% dos estudantes, sendo que essas duas alternativas de resposta apresentavam uma associação correta de apenas dois algarismos as suas respectivas ordens.
Vale destacar que, mediante o nível de proficiência de sua turma, o professorado poderá propor variações desse item, visando aumentar o grau de complexidade da tarefa apresentada. Uma possibilidade é a sugestão de novos distratores, fazendo uso dos algarismos que compõem o número na ordem em que esses aparecem na escrita do número, porém, relacionados a ordens diferentes das corretas. Como é o caso do exemplo a seguir:
Observe o seguinte número:
1325
A decomposição desse número está apresentada em
(A) 1 unidade, 3 dezenas, 2 centenas e 5 unidades de milhar.
(B) 1 unidade, 3 centenas, 2 dezenas e 5 unidades de milhar.
(C) 1 unidade de milhar, 3 centenas, 2 dezenas e 5 unidades.
(D) 1 unidade de milhar, 3 dezenas, 2 centenas e 5 unidades.
Nesse caso, ao ser capaz de descartar as alternativas incorretas, o estudante demonstra maior clareza sobre a temática. Enquanto no formato original da questão basta verificar se os algarismos apresentados nas alternativas estão na mesma sequência do número 1325, no caso desse novo formato de item, além de verificar essa característica, é necessário que o respondente indique qual a ordem correta associada a cada algarismo que forma o número.
Essa necessidade de averiguar não somente a ordem da disposição dos algarismos, mas se certificar das ordens associadas a cada um deles também visa corrigir equívocos na decomposição polinomial de números, principalmente no Grupo de Menor Desempenho, que apresenta índices de acerto mais tímidos. Por exemplo, para quase 30% dos estudantes desse Grupo, a decomposição do número 325 pode ser a seguinte: 3 x 1 + 2 x 10 + 5 x 100. Isso indica que há uma preocupação com a ordenação dos algarismos, mas não com a ordem associada a cada um deles.
Por outro lado, ao longo da prova de 2021, foram propostos outros itens relacionados a essa habilidade e que trazem maiores informações de desenvolvimento da mesma. São elas:
- A inserção do algarismo zero na escrita do número eleva o grau de dificuldade, sendo observados equívocos como:
- O número 2 305 ser decomposto como 2 x 1 000 + 3 x 100 + 0 x 10 + 5 x 0;
- O número 1 906 ser decomposto como 1 000 + 90 + 6;
- A decomposição 2 unidades de milhar, 0 centenas, 3 dezenas e 5 unidades ser associada aos números 2 000 305 ou 2 503.
- Confusão entre a ordem da unidade de milhar e das centenas, ao apontar, por exemplo, que no número 2 531, o algarismo da centena é o 2.
- Dificuldade em determinar o número a partir de sua decomposição, quando não é informada a ordem que está relacionada ao algarismo zero. Um caso que retrata essa dificuldade é, por exemplo, a identificação do número atrelado a seguinte decomposição numérica: 2 unidades de milhar, 5 centenas e 3 dezenas. Nesse exemplo, cabe destacar, que mais de um quarto dos respondentes aponta que essa decomposição corresponde ao número 235, ou seja, um número composto por 3 algarismos e que, portanto, sequer possui um algarismo da ordem de unidade de milhar.
Reconhecer as propriedades do Sistema de Numeração Decimal é fruto de um conjunto de habilidades que demonstraram requerer aprimoramento. Nessa fase de retomada é muito importante explorar aquilo que, de fato, os estudantes já conhecem para então buscar ampliar essas ideias, a partir do estabelecimento de novas relações.
|
 |
Exemplo 2
Nível Básico
Compõe a descrição do ponto 200 da Escala de Matemática – SARESP
H06 Identificar fração como representação que pode estar associada a diferentes significados (parte/todo, quociente, razão).
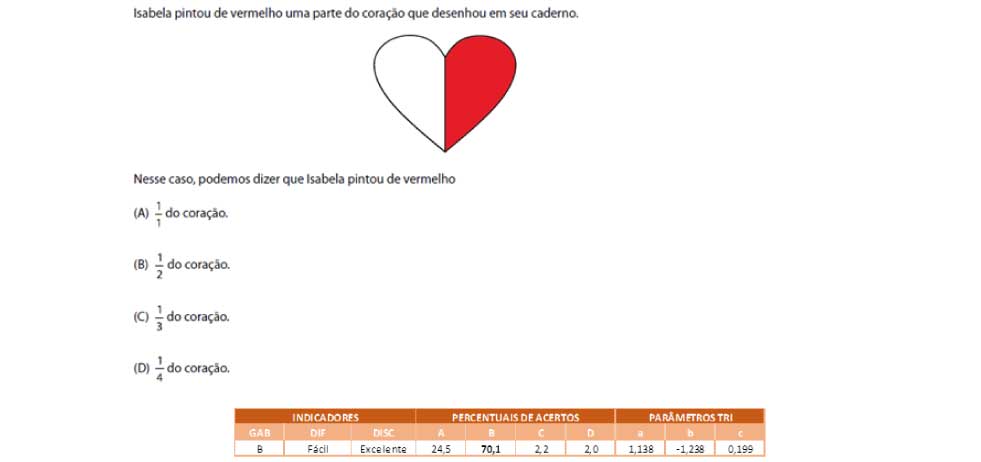
O item apresentado envolve a utilização da fração como representação da relação parte-todo. O objetivo era que o respondente analisasse a imagem e determinasse a fração do desenho que está pintada de vermelho. Nesse caso, temos que metade do coração está pintado de vermelho, o que pode ser representado pela fração  . Juntamente com a investigação da obtenção da fração, é importante aferir se os estudantes conseguem compreender a ideia de metade empregada na frase anterior.
Esse item foi acertado por praticamente 7 em cada 10 respondentes, sendo classificado como um item Fácil. Ao analisar os índices de acerto dos Grupos de Menor e Maior Desempenho, observa-se que o item possui uma qualidade excelente de discriminação, uma vez que no Grupo de Menor Desempenho o índice de acerto é de 41,2% enquanto que no Grupo de Maior Desempenho esse percentual é de 93,2%.
Ainda cabe apontar que dentre aqueles que erraram o item, a imensa maioria optou pela alternativa (A), sendo que no Grupo de Menor Desempenho essa alternativa de resposta foi mais escolhida que o gabarito. A motivação para a escolha dessa alternativa (A) 1/1 como opção de resposta possivelmente está relacionada com a não compreensão ou desconhecimento do conceito parte-todo. A escolha pela fração 1/1 sugere que os estudantes estão contando a quantidade de partes vermelha e “não vermelhas” (brancas, no caso) e montando a fração a partir desses números obtidos.
Vale lembrar que a razão  está associada a outras relações parte-todo equivalentes, de modo que essa fração também pode ser usada para representar casos como:
Todas essas figuras, quando sobrepostas umas sobre as outras, têm a mesma região pintada de vermelho, ou seja, todas elas possuem uma metade vermelha. Assim sendo, a fração que representa a parte vermelha de todas essas figuras é  .
Provavelmente, que em um primeiro momento, o alunado faça uso de outras frações para representar as regiões vermelhas das figuras, como  ou  ou 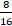 , todas elas baseadas numa ideia de contagem das partes e do todo. A ideia é que ao mostrar que as figuras quando sobrepostas possuem a mesma região vermelha, os estudantes possam reconhecer que todas essas frações representam a mesma razão e, por isso, são chamadas de equivalentes, de modo que qualquer uma delas pode ser utilizada para representar a razão de todas as figuras.
É importante que os estudantes passem a considerar as frações equivalentes como meio de representar uma razão, de modo a não ficarem dependentes da contagem das partes. Essa estratégia calcada na contagem das partes também foi a provável causa do erro de boa parte do alunado num outro item da prova de 2021 que trazia a seguinte figura:
O objetivo, mais uma vez, era obter a fração que representava a parte vermelha da figura. A imensa maioria (70,9%) optou pela fração  para representar a parte vermelha. Mesmo no Grupo de Maior Desempenho, essa alternativa de resposta foi assinalada por 62,6%, ou seja, quase dois terços desse grupo de melhor desempenho na prova não foi capaz de mobilizar seus conhecimentos e assinalar a fração  , resposta dada por apenas 11,6% dos estudantes que resolveram a prova.
Cabe lembrar também que em edições anteriores da prova SARESP uma dificuldade comum observada era a utilização de números decimais para representar razões. No caso de figuras como as apresentadas aqui era comum observar equívocos como:
Considerar que os números utilizados na escrita da fração  são os mesmos presentes na escrita do número decimal, de modo a sinalizarem o decimal 1,2 como resultado da razão procurada.
Estabelecer correlação entre as partes pintadas de vermelho (4) e a escrita do número decimal, optando por 0,4 como resultado da razão procurada.
Por fim, mais do que a capacidade de obter escritas equivalentes para representar razões, a noção de equivalência acaba por ser um facilitador na compreensão e execução de cálculos envolvendo quantidades não inteiras, muito comum nos anos seguintes do Ensino Fundamental.
|
|
Exemplo 3
Nível Adequado
Compõe a descrição do ponto 250 da Escala de Matemática – SARESP
H25 Estabelecer relações entre unidades de medida de tempo.
O item proposto envolve determinar o horário de início do preparo de uma refeição, dado que o horário programado para servi-la é meio-dia e que o tempo necessário para que o prato fique pronto é de 2 horas e 40 minutos. Para obter a resposta correta é preciso associar o termo meio-dia a 12h00 e então descontar 2 horas e 40 minutos.
Importante que os estudantes saibam que a maneira de resolver subtração envolvendo períodos de tempo é diferente daquela usual, empregada para números naturais e decimais, uma vez que o sistema de horas e minutos não segue as regras do sistema decimal de numeração.
Conforme apontado anteriormente, a obtenção da resposta correta demanda descontar 2 horas de 12:00, resultando em 10:00, para então descontar os 40 minutos faltantes. Nesse caso, será feita uma ideia de recurso, similar à empregada na subtração entre números naturais, porém, ao invés de 1 hora “emprestar 10”, uma hora “emprestará 60” minutos. Sendo assim, uma ideia para finalizar o problema é a seguinte:
Precisamos fazer 10 horas - 40 minutos
Sabemos que 10 horas = 9 horas + 60 minutos
Então, fazemos 9 horas + 60 minutos - 40 minutos, obtendo 9 horas e 20 minutos
Além dessa solução, os estudantes também poderiam encontrar a resposta correta por meio de estimativa, uma vez que o tempo de preparo é superior a 2 horas. Com isso, o início da preparação do prato deve ocorrer antes das 10h00 (duas horas antes do meio-dia) e há apenas uma opção de resposta com horário anterior a este.
O item foi respondido corretamente por menos da metade (44,9%) dos respondentes, caracterizando a tarefa como mediana, em nível de dificuldade. Além disso, essa questão apresentou excelente índice de discriminação, uma vez que os índices de acerto nos Grupos de Menor e Maior Desempenho foram de 20,7% e 73,7%, respectivamente.
Ao analisar os distratores do item, temos que a alternativa (C) foi a opção de 27,4% dos respondentes, indicando que esses estudantes provavelmente fizeram apenas a subtração das horas e ignoraram os minutos. Já a alternativa (B) foi a escolha de um em cada oito respondentes, mas essa escolha provavelmente se baseia apenas no desconto de 40 minutos, ignorando as 2 horas, ou então na associação incorreta de meio dia com algum outro horário diferente de 12h00. Por fim, a alternativa (A), assinalada por 14,1% dos respondentes, apresenta o horário relacionado a meio-dia, indicando que a tarefa a ser executada não deve ter sido compreendida por esse grupo de respondentes. Cabe destacar que a alternativa (A) foi a opção de resposta mais escolhida pelos estudantes do Grupo do Menor Desempenho.
Outro item de tarefa similar a essa se mostrou ainda mais difícil para o grupo de respondentes, o que se deve, provavelmente, ao fato de que o tempo a ser descontado foi dado apenas em minutos, e não em horas e minutos como no caso apresentado. A tarefa consistia em determinar o horário de início de um evento, dado que esse evento terminou às 12 horas e que o mesmo durou 110 minutos. O índice de acerto foi inferior a um terço (30,9%), sendo que mesmo no Grupo de Maior Desempenho o índice de acerto não chegou a 36%, ficando próximo de ser classificado como um item de difícil.
Ao analisar os distratores desse segundo item, observa-se que a conversão de 110 minutos para 1 hora e 50 minutos não está clara para a maioria dos estudantes, pois o distrator mais assinalado sugere que os estudantes estão associando 110 minutos a 1 hora e 10 minutos, indicando uma confusão no uso da base sexagesimal na conversão minuto–hora. Além do mais, há aqueles que também estão errando na execução do cálculo, ao fazer 12h00 – 1h10 = 11h10. Nesse caso, é provável que os respondentes estejam subtraindo o menor algarismo do maior, não importando a posição de cada um no cálculo.
Um terceiro item que também investigou essa tarefa de “voltar no tempo” envolvia a identificação do horário de um encontro que ocorreu 10 minutos antes das 20h. Esse item, mais simples que os anteriores, alcançou 74% de acerto, sendo que o distrator mais escolhido traz uma informação relevante, não observada nos itens anteriores: parte dos estudantes, principalmente aqueles do Grupo de Menor Desempenho (30% aproximadamente), invertem o significado do termo “antes”, indicando como resposta o horário de 20h10, ou seja, 10 minutos depois das 20h.
Em outras tarefas associadas a conversão de unidades de medida de tempo e resolução de problemas, os estudantes tiveram o seguinte desempenho:
- Reconhecer que 60 minutos corresponde a 1 hora – 78% de acerto geral, mas no Grupo de Menor Desempenho esse índice se reduz para 45,2%.
- Associar 90 minutos a 1 hora e 30 minutos – 62,8% de acerto geral, sendo que, no Grupo de Menor Desempenho, a distribuição das escolhas nas alternativas de resposta sugere uma escolha quase que aleatória da resposta por esse grupo, pois ficaram muito divididos de maneira muito próxima entre as quatro alternativas de resposta.
- Identificar o relógio de ponteiros que está marcando corretamente 16:00 – 60,9% de acerto geral, sendo que a indicação de 6 horas da tarde foi o distrator mais frequente, possivelmente pela presença do algarismo 6, sendo essa a opção de resposta mais assinalada no Grupo de Menor Desempenho.
- Transformar 12 semanas em dias – 58,8% de acerto geral, sendo que o principal distrator estabelecia a correspondência de 12 semanas com 60 dias, muito provavelmente pelo fato de o problema tratar de um contexto de trabalho, fazendo com que os respondentes considerassem apenas 5 dias por semana.
Reconhecer o horário mostrado em um relógio digital que marca 25 minutos para às 8 horas da noite – 58,6% de acerto geral, tendo alto índice de discriminação, uma vez que no Grupo de Menor Desempenho foi observado 26,7% de acerto, enquanto que no Grupo de Maior Desempenho esse percentual foi de 87,6%. |
|
|
|
|
 |
|
