|
|  |
Nessa edição de 2021 da prova SARESP para o 3º ano do Ensino Fundamental, diferente das versões anteriores, as questões objetivas tiveram papel central na composição do instrumento avaliativo. Para análise dos resultados, esse é um fator que deve ser levado em consideração, pois se trata de um modelo diferente de prova e seu formato pode ser desafiador aos estudantes nesse primeiro contato. Pela mudança no tipo de questões da prova não é viável estabelecer certas comparações entre essa edição e edições anteriores.
Além dessa mudança, é importante frisar a singularidade das condições de aprendizagem dos estudantes que participaram dessa edição nesses últimos dois anos devido a pandemia de Covid-19 e precisam ser levadas em consideração na análise dos resultados. Desde os primeiros meses de 2020, devido a necessidade do distanciamento social imposta pela pandemia, a dinâmica escolar foi completamente alterada e apresentou diversos desafios aos profissionais da educação, aos estudantes e seus familiares. Especificamente sobre os estudantes do 3º ano, reforçamos que frequentaram o Ensino Fundamental regularmente quando estavam no 1º ano. Porém, tanto no 2º como no 3º ano o ensino presencial ocorreu por pouco tempo e em situação diferente do que foi vivenciada até o ano de 2019 – mesmo com o retorno, muitos cuidados ainda eram necessários, impondo às escolas, além da preocupação com a aprendizagem, pensar estratégias que garantissem a preservação da vida nesse cenário.
Durante esses dois anos, repletos de incertezas, propostas de ensino remoto e interações virtuais passaram a ser a nova realidade das escolas e os professores precisaram descobrir novas formas de promover a aprendizagem dos seus estudantes, contando ainda mais com a parceria das famílias.
Dentre tantos desafios, especificamente sobre o ensino da Matemática nos Anos Iniciais, sabemos da importância da mediação dos professores e das práticas de sala de aula para a aprendizagem que envolvem o uso de materiais manipulativos, proposições de situações concretas, vivências de jogos, entre outras possibilidades, que acabaram sendo inviabilizadas durante o período pandêmico.
Dúvidas e angústias marcaram esse período – a incerteza de quanto tempo o distanciamento seria necessário e consequentemente o ensino remoto, a adaptação ao novo contexto, dificuldades materiais e tecnológicas, como falta de aparelhos adequados para que os estudantes pudessem acompanhar as aulas, problemas de conexão de internet, entre outras tantas questões específicas a cada região do estado de São Paulo.
Esse panorama ressalta a importância de uma avaliação sistematizada como o SARESP, que possibilita mais um olhar diagnóstico da aprendizagem, trazendo informações importantes a serem refletidas pela comunidade escolar. Tais reflexões podem contribuir para o planejamento de ações futuras, visando fortalecer o ensino e focalizar problemáticas a serem sanadas”.
PARTE 1 – ITENS DE RESPOSTA CONSTRUÍDA
A prova do 3º ano EF também contou com a aplicação de questões de respostas construídas, sendo a correção destas feita apenas com um grupo amostral. A seguir apresentaremos as questões, os critérios de correção e faremos uma breve discussão a respeito dos objetivos de cada uma delas. Há duas versões de cada questão, de acordo com o período.
Para os estudantes do 3º ano do Ensino Fundamental também foram propostas duas questões de respostas construídas, porém ambas com duas partes.
A primeira questão se aproxima da segunda proposta ao 2º ano, mas no caso do 3º ano, foi apresentado apenas o resultado dos cálculos, cabendo aos estudantes uma vasta possibilidade de respostas. A ausência de um número para se ancorar no cálculo pode se revelar um desafio aos estudantes pequenos.
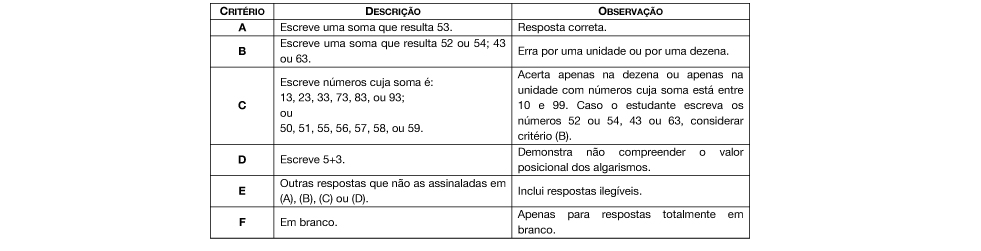
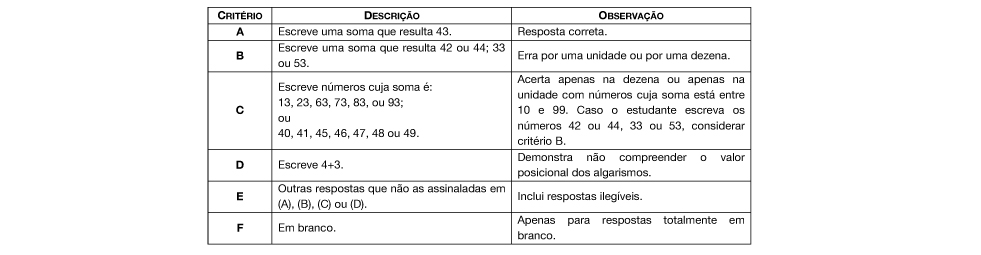
Na primeira parte da questão os estudantes deveriam indicar dois números que quando somados resultassem em 53 (ou 43 na versão da tarde). As possibilidades são as mais variadas, sendo, geralmente, as mais frequentes: 50 + 3; 52 + 1; 53 + 0; 43 + 10 (ou 40 + 3; 42 + 1; 43 + 0; 33 + 10 na versão da tarde). Também é possível observar que algumas crianças optaram por escolher um número aleatório para a primeira parcela e a partir dele contar quanto era necessário para chegar ao resultado.
Alguns estudantes possivelmente indicaram a soma 5 + 3 (ou 4 + 3 na versão da tarde), revelando que apenas separaram os números do resultado, não compreendendo ainda que o algarismo 5 representa nesse caso 5 dezenas, ou seja, o número 50.
Na segunda parte dessa questão, os estudantes deveriam indicar dois números que, quando subtraídos resultavam em 15 (ou 25 na versão da tarde). Assim como na primeira parte da questão, há uma infinidade de possibilidades de respostas. As que provavelmente mais apareceram foram: 20 – 5; 30 – 15; 15 – 0; 16 – 1 (ou 30 – 5; 40 – 15; 25 – 0; 26 – 1 na versão da tarde).
O estudante precisava se atentar, sobretudo, se tratar de uma subtração, e por isso o maior número deveria ser o minuendo e o menor o subtraendo, havendo casos em que houve a inversão e, por isso, chegaram ao resultado –15 (ou –25).
Veja a seguir a questão e seus critérios de correção:
Versão Manhã:

Critérios de correção:
PARTE A
PARTE B

Versão Tarde:

Critérios de correção:
PARTE A
PARTE B

A segunda questão apresentada aos estudantes do 3º ano abordava sequências numéricas que deveriam ser completadas de acordo com o padrão.
Na parte A, a sequência era crescente, aumentando de 5 em 5. Nesse caso, os estudantes deveriam determinar os dois próximos números da sequência dada. Na versão da manhã, o último número apresentado foi o 125, cabendo aos estudantes indicarem como resposta os números 130 e 135. Já na versão da tarde o último número era o 135 e, por isso, a resposta correta seria 140 e 145.
Era esperado que alguns estudantes não percebessem de quanto em quanto a sequência estava aumentando e por isso indicarem como respostas 126 e 127 (ou 136 e 137 para a versão da tarde) ou ainda, aumentarem de 2 em 2, apresentando como resposta 127 e 129 (ou 137 e 139).
Já na parte B, a sequência apresentada era decrescente e estava diminuindo de 10 em 10. Além disso, os estudantes, dessa vez, deveriam determinar o primeiro e o último termo da sequência.
Determinar o primeiro termo pode se revelar desafiador às crianças, pois ao perceber o padrão da sequência, precisa fazer o cálculo inverso ancorada no segundo termo. Por exemplo, na versão da manhã, o segundo número da sequência é o 90 e para determinar o primeiro número ela precisa somar 10 e não subtrair, uma vez que o número a ser descoberto vem antes. Por esse motivo, pode ter sido recorrente que estudantes indicassem o 80 como primeiro termo, mesmo esse número já aparecendo na sequência.
Veja as questões e seus respectivos critérios de correção:
Versão Manhã:

Critérios de correção:
PARTE A

PARTE B

Versão Tarde:

Critérios de correção:
PARTE A

PARTE B

PARTE 2 – ITENS DE MÚLTIPLA ESCOLHA
A Matriz de Referência para o SARESP traz um conjunto de habilidades que servem para nortear a montagem das provas do 5ºEF, 9ºEF e 3ªEM. Contudo, esse documento oficial, que data de 2009, não apresenta um conjunto de habilidades para os anos iniciais do Ensino Fundamental.
Em vista disso, ao longo dos anos, as provas do 2ºEF e 3ºEF foram sendo construídas com base no Currículo Paulista, consolidando um rol de habilidades recorrentes na elaboração dessas provas. Na edição de 2021, devido ao aumento do número de questões objetivas, esse rol precisou ser ampliado. Para tanto, foram privilegiadas as habilidades essenciais, uma vez que estas consideram as adequações pensadas pela Secretaria de Educação frente aos impactos escolares decorrentes da pandemia de Covid-19.
Em suma, os itens propostos utilizados na composição das provas do 2ºEF e 3ºEF do SARESP 2021 são baseados num histórico, que assegura melhor comparabilidade nos resultados de diferentes edições, e na realidade escolar da rede estadual, ao se nortear pelas habilidades do Currículo Paulista indicadas como essenciais pela SEDUC.
Nessa edição de 2021 da prova SARESP para o 3º ano do Ensino Fundamental, diferente das versões anteriores, as questões objetivas tiveram papel central na composição do instrumento avaliativo. Para análise dos resultados, esse é um fator que deve ser levado em consideração, pois se trata de um modelo diferente de prova e seu formato pode ser desafiador aos estudantes nesse primeiro contato. Pela mudança no tipo de questões da prova não é viável estabelecer certas comparações entre essa edição e edições anteriores.
Além dessa mudança, é importante frisar a singularidade das condições de aprendizagem dos estudantes que participaram dessa edição nesses últimos dois anos devido a pandemia de Covid-19 e precisam ser levadas em consideração na análise dos resultados. Desde os primeiros meses de 2020, devido a necessidade do distanciamento social imposta pela pandemia, a dinâmica escolar foi completamente alterada e apresentou diversos desafios aos profissionais da educação, aos estudantes e seus familiares. Especificamente sobre os estudantes do 3º ano, reforçamos que frequentaram o Ensino Fundamental regularmente quando estavam no 1º ano. Porém, tanto no 2º como no 3º ano o ensino presencial ocorreu por pouco tempo e em situação diferente do que foi vivenciada até o ano de 2019 – mesmo com o retorno, muitos cuidados ainda eram necessários, impondo às escolas, além da preocupação com a aprendizagem, pensar estratégias que garantissem a preservação da vida nesse cenário.
Durante esses dois anos, repletos de incertezas, propostas de ensino remoto e interações virtuais passaram a ser a nova realidade das escolas e os professores precisaram descobrir novas formas de promover a aprendizagem dos seus estudantes, contando ainda mais com a parceria das famílias.
Dentre tantos desafios, especificamente sobre o ensino da Matemática nos Anos Iniciais, sabemos da importância da mediação dos professores e das práticas de sala de aula para a aprendizagem que envolvem o uso de materiais manipulativos, proposições de situações concretas, vivências de jogos, entre outras possibilidades, que acabaram sendo inviabilizadas durante o período pandêmico.
Dúvidas e angústias marcaram esse período – a incerteza de quanto tempo o distanciamento seria necessário e consequentemente o ensino remoto, a adaptação ao novo contexto, dificuldades materiais e tecnológicas, como falta de aparelhos adequados para que os estudantes pudessem acompanhar as aulas, problemas de conexão de internet, entre outras tantas questões específicas a cada região do estado de São Paulo.
Esse panorama ressalta a importância de uma avaliação sistematizada como o SARESP, que possibilita mais um olhar diagnóstico da aprendizagem, trazendo informações importantes a serem refletidas pela comunidade escolar. Tais reflexões podem contribuir para o planejamento de ações futuras, visando fortalecer o ensino e focalizar problemáticas a serem sanadas.
De maneira geral, os níveis de proficiência atingidos pelos estudantes do 3º ano foram: 27,3% ficaram no nível abaixo do básico, 38,4% conseguiram índices correspondentes ao nível básico, 23,8% chegaram ao nível adequado e 10,5% alcançaram índices considerados avançados.
Podemos enfatizar que a soma dos níveis básico e adequado corresponde ao nível satisfatório, ou seja, 62,2% dos estudantes atingiram os objetivos traçados para esse ano escolar. Tal porcentagem acrescida do nível avançado abarcou pouco mais de 70% dos respondentes e ao se considerar o contexto pandêmico discutido anteriormente e as condições de ensino-aprendizagem se revelou um bom resultado. Porém, os quase 30% que ficaram no nível abaixo do básico, ou seja, obtiveram um resultado insatisfatório a essa etapa escolar, correspondem a um número significativo de crianças e merecem um olhar cuidadoso da comunidade escolar em relação a aprendizagem matemática.
A percepção dos estudantes, em relação ao grau de dificuldade dos itens, oscilou entre fácil e média e está destacada na tabela a seguir:
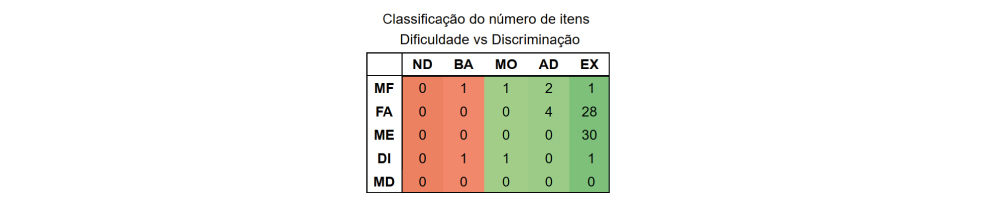
[Nota: Dificuldade: Muito Fácil (MF); Fácil (FA); Médio (ME); Difícil (DI) e Muito Difícil (MD) e Discriminação: Não Discrimina (ND); Baixa (BA); Moderada (MO) Adequada (AD) e Excelente (EX)].
De maneira geral, pode-se afirmar que os estudantes apresentaram facilidade principalmente em itens envolvendo identificação da unidade de medida correta, situações-problema envolvendo cálculos do campo aditivo que não necessitavam de reagrupamento, reconhecimento do maior número dentre os apresentados, comparação entre figuras geométricas e suas nomenclaturas ou suas planificações, leitura de gráficos e tabelas em questões envolvendo preferências e reconhecimento do valor de cédulas e moedas. Questões que abordaram ideias de multiplicação ou divisão revelaram-se mais desafiadoras, assim como itens envolvendo medidas de tempo, leitura de calendário, deslocamento em mapas e cálculos com reagrupamento.
A seguir, apresentamos quatro questões da prova para ilustrar o desempenho dos estudantes em itens ancorados em diferentes pontos da escala de proficiência. Atrelado a esses itens, tecemos observações gerais do desempenho dos estudantes na prova, principalmente para casos em que possíveis erros foram constatados, o que traz informações relevantes para reflexão e orientação de trabalho dos professores da rede estadual.

EXEMPLO 1
Nível Abaixo do Básico
Compõe a descrição do ponto 125 da Escala de Matemática – SARESP
(EF03MA14) Descrever características de algumas figuras geométricas espaciais (prismas retos, pirâmides, cilindros, cones), relacionando-as com suas planificações.
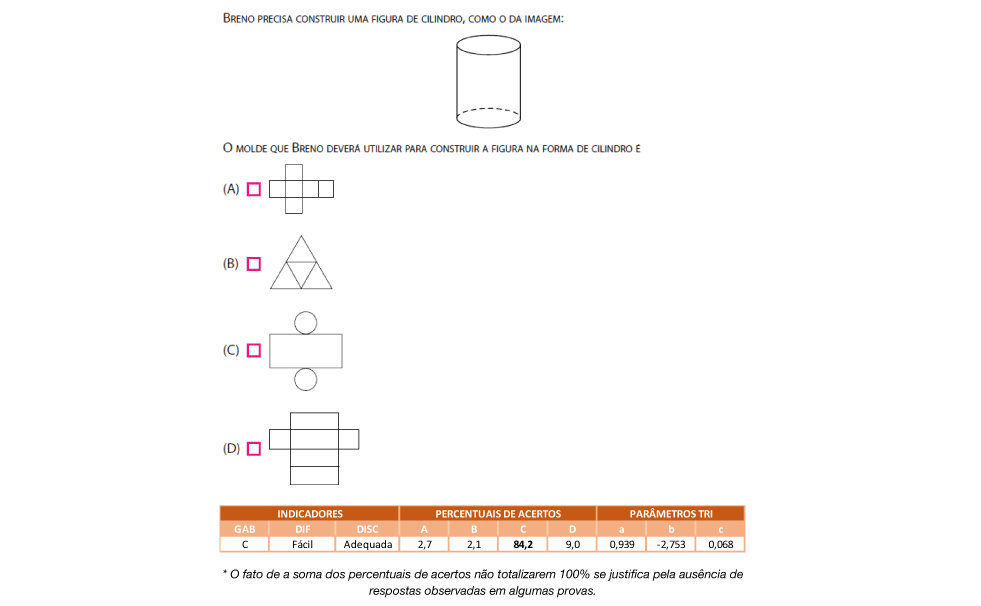
O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Abaixo do Básico. A tarefa envolve relacionar um cilindro ao seu molde (planificação), sendo que dentre as alternativas, apenas a planificação correta possuía círculos.
Responderam corretamente esse item cerca de 84,2% dos estudantes, indicando que esse conhecimento já foi apropriado pela maioria dos estudantes. As alternativas A (planificação do cubo) e B (planificação de uma pirâmide de base triangular) tiveram cerca de 2% das respostas cada uma. Já a alternativa D (planificação de um bloco retangular) foi a opção de 9% dos respondentes, provavelmente por ser uma das figuras geométricas mais abordadas nos anos iniciais, revelando que esses estudantes ainda não fazem a correspondência entre as faces do sólido e as formas da planificação, pois tal alternativa seria facilmente excluída, assim como a A e B, ao se observar a ausência dos círculos das bases do cilindro.
Cabe destacar que, assim como no 2º ano EF, tarefas envolvendo habilidades ligadas a geometria que envolvem competências cognitivas atreladas ao reconhecer foram observadas nos pontos mais baixos da escala de proficiência, indicando que essas tarefas são menos complexas e devem ser consideradas como pontos de partidas para o desenvolvimento de outras mais complexas. Como dito anteriormente, para esse item, apenas a alternativa correta trazia círculos, o que pode ter sido um facilitador. Nesse caso, é importante investigar, por exemplo, se a planificação de um cone estivesse entre as opções de resposta se ela atrairia parte daqueles que acertaram essa questão.
Esse tipo de alteração no item pode ser realizado na sala de aula pelos professores, a fim de ampliar as informações que subsidiarão eventuais decisões para o desenvolvimento das aulas seguintes.

EXEMPLO 2
Nível Básico
Compõe a descrição do ponto 175 da Escala de Matemática – SARESP
(EF03MA06) Resolver e elaborar problemas de adição e subtração com os significados de juntar, acrescentar, separar, retirar, comparar e completar quantidades, utilizando diferentes estratégias de cálculo exato ou aproximado, incluindo cálculo mental.

O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Básico. Trata da resolução de uma situação-problema envolvendo adição com reserva (composição) para determinar o total de pontos obtidos por dois times que participaram de uma competição, sendo a pontuação de ambos um número de ordem das centenas.
Ao analisar o desempenho das crianças, destaca-se que a alternativa correta foi assinalada por 59,1% dos estudantes, pouco mais da metade. As demais alternativas receberam quantidades de indicações aproximadas dos estudantes, revelando que os três erros presentes nessas respostas merecem um olhar atento dos professores no trabalho com adições com reserva.
Na alternativa A, assinalada por 13,9% dos respondentes, o erro provável foi que os estudantes esqueceram de somar a dezena resultante da soma das unidades (o “sobe um”), possivelmente por desatenção.
Já na alternativa C, indicada por 10,7% das crianças, o erro provável foi que a dezena resultante da soma das unidades, na verdade, foi alocada na ordem da centena, o que requer um afinamento no trabalho com a correspondência entre cada ordem. A manipulação do material dourado envolvendo situações de troca entre as ordens, por exemplo, facilita a compreensão das crianças nesse sentido.
A alternativa D, que foi escolhida por 13% dos estudantes merece um pouco mais de atenção – ao realizar o cálculo através do algoritmo, o estudante coloca a soma das unidades direto na resposta, não respeitando a regra de apenas um algarismo em cada ordem numérica, alterando completamente o resultado. Percebe-se nesse caso que a criança provavelmente não ponderou sobre a plausibilidade do resultado do seu cálculo, que deu um número muito maior do que o esperado. Mais do que compreender a sistemática do algoritmo da adição, que requer seguir um apanhado de regras, é fundamental que o estudante compreenda o funcionamento do Sistema Decimal de Numeração e consiga estabelecer relações numéricas, estimar resultados possíveis antes de realizar o cálculo, no intuito de conseguir perceber se o resultado encontrado é plausível ou não, pois não faz sentido somar dois números um pouco maiores do que cem e obter um resultado maior que dois mil como resposta. Assim, todos os erros apresentados necessitam de algum tipo de trabalho para que os estudantes avancem e superem essas dificuldades, mas as crianças que optaram pela alternativa D, provavelmente, são as que requerem um olhar mais atento dos professores e investimentos em propostas que auxiliem na construção do entendimento de números.

EXEMPLO 3
Nível Adequado
Compõe a descrição do ponto 200 da Escala de Matemática – SARESP
(EF03MA05) Utilizar diferentes procedimentos de cálculo mental e escrito para resolver problemas significativos envolvendo adição, subtração e multiplicação com números naturais.

O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Adequada. Requer que o estudante resolva um problema envolvendo multiplicação (soma de parcelas iguais) para determinar quantos tentáculos há em um aquário, dada a quantidade de polvos nesse aquário e que cada polvo possui 4 tentáculos.
Os números do enunciado viabilizavam diferentes estratégias de cálculo: soma sucessivas de parcelas, registro pictórico, entre outras. O desempenho dos estudantes nesse item e em outros que também envolviam a ideia multiplicativa foi muito parecido, apresentaram uma média de 55% de acerto. Especificamente nesse item apresentado, 52,4% dos estudantes calcularam corretamente a quantidade de tentáculos no aquário onde havia 4 polvos. Se considerarmos apenas os estudantes do Grupo de Maior Desempenho1, o índice de acerto sobe para quase 76%, enquanto que no Grupo de Menor Desempenho, esse percentual baixa para aproximadamente 16%, o que mostra que esse item foi excelente para diferenciar o desempenho desses dois grupos.
As alternativas B (24) e D (48) tiveram o mesmo índice – 8,8%. Na alternativa B, provavelmente, a criança se perdeu na contagem e acabou calculando a quantidade de tentáculos de um polvo a menos do que o pedido (8 x 3). Já na alternativa D, uma possibilidade é que o estudante tenha somado os números do enunciado (8 + 4 = 12) e depois multiplicado esse resultado por 4 (12 x 4 = 48), ou simplesmente se perdeu nas contagens sucessivas do 8 e indicou a maior alternativa.
A alternativa A (12) chama a atenção pelo número significativo de crianças que a escolheram – 26,7%. Provavelmente, os estudantes que optaram por essa resposta, não compreenderam a situação proposta e somaram os números que aparecem no enunciado. Em outros itens que envolviam a ideia multiplicativa, foi recorrente a alternativa errada mais indicada ser a soma dos números do enunciado. Estimular os estudantes a desenharem a situação proposta pode ser um caminho para auxiliar na compreensão da resolução de problemas. Mas, infelizmente, muitas vezes, observamos que há um movimento precipitado de incentivo para que as crianças abandonem essa estratégia tão importante, que possibilita a reflexão sobre o problema.
Frente a isso, ressalta-se mais uma vez a importância o estímulo para a variação das estratégias utilizadas na resolução de problemas, evitando colocar determinadas opções acima de outras. Igualmente importante é o respeito ao tempo de aprendizagem de cada estudante, de modo a considerar as potencialidades e necessidades de criança, evitando atropelos que acarretarão em dificuldades para o desenvolvimento de habilidades matemáticas futuras.
1. O grupo de maior desempenho é formado por 27% dos respondentes e inclui aqueles que obtiveram os maiores números de acertos gerais na prova. Analogamente, o grupo de menor de desempenho também é constituído por 27% dos respondentes, que tiveram os menores índices de acerto geral na prova.

EXEMPLO 4
Nível Avançado
Compõe a descrição do ponto 250 da Escala de Matemática – SARESP
(EF03MA23) Ler horas em relógios digitais e em relógios analógicos e reconhecer a relação entre hora e minutos e entre minuto e segundos.

O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Avançada. O estudante precisava realizar a leitura de um relógio de ponteiro, indicando que a hora apresentada é 10 horas e 10 minutos.
Em relação ao desempenho nesse item, 32,8% dos estudantes indicaram a alternativa correta, ou seja, menos de um terço dos estudantes conseguiu executar a tarefa proposta. A alternativa C (10 horas e 2 minutos) foi a segunda mais indicada, contando com 29,7% das respostas do alunado, índice muito próximo da alternativa correta, revelando que a leitura dos minutos no relógio de ponteiro foi desafiadora para o público da prova.
A alternativa B (2 horas e 10 minutos) também teve um índice relevante – 23,7% escolheram essa opção. Nesse caso, os estudantes inverteram os ponteiros, atribuindo o grande para as horas e o pequeno para os minutos, além de fazer a leitura “literal” dos minutos, ou seja, não compreenderam que o número 10 mostrado no relógio indica 50 minutos.
A alternativa A (2 horas e 50 minutos) foi indicada apenas por 6,8% dos respondentes, provavelmente porque os 50 minutos não ficam evidentes no relógio e por isso, não foi uma alternativa tão atrativa como a B.
Possivelmente esse não foi um conteúdo muito abordado em situação de ensino remoto. É comum os próprios estudantes pedirem para aprender a leitura de relógio de ponteiro quando têm contato com esse tipo de aparelho, diante do desejo de regularem a sua rotina escolar (que horas será o recreio, quanto tempo falta para a aula de Educação Física). Tais situações não foram vivenciadas no período pandêmico, mas com o retorno das aulas presenciais e o contato com esse tipo de relógio, esse conhecimento pode ser apropriado por esses estudantes.
|
 |
|
|
|

|
