|
|
 |
Exemplo 1
Nível Abaixo do Básico
Compõe a descrição do ponto 250 da Escala de Matemática – SARESP
H37 Calcular e interpretar medidas de tendência central de uma distribuição de dados (média, mediana e moda) e de dispersão (desvio padrão).

O item caracteriza uma tarefa realizada corretamente por estudantes que possuem proficiência classificada como Abaixo do Básico. A tarefa envolve determinar a moda estatística de um conjunto de dados apresentados. A definição do conceito está presente no enunciado, fazendo com que o respondente não precise lembrar-se dessa definição, evitando assim que ele se confunda com as definições de média ou mediana.
Ao analisar os números listados, observa-se que o número 39 é o único que aparece mais de duas vezes e, portanto, deve ser considerado a moda estatística desse rol de números apresentados. Essa tarefa foi executada corretamente por aproximadamente 7 em cada 10 respondentes, sendo que a alternativa correta foi a opção mais assinalada em todos os grupos de desempenho. No entanto, no grupo de menor desempenho, menos da metade (48%) foi capaz de reconhecer a moda estatística corretamente. Importante destacar que, nesse grupo, 15% dos estudantes optaram pelo maior número da lista como sendo a moda estatística, indicando que a definição dada no enunciado não foi devidamente compreendida.
Também é importante destacar que quase 7% dos respondentes indicar a alternativa (D) como resposta correta, sendo que o número 38 sequer está presente no rol listado, indicando que esse contingente de estudantes, de fato, não deve conhecer o conceito de moda, uma vez que, diferentemente da média e da mediana, a moda obrigatoriamente deve ser um dos números listados.
Outros itens presentes na avaliação de 2021, relacionados as medidas de tendência central, também trouxeram informações relevantes sobre a aprendizagem dos estudantes da rede estadual. Ao analisar o desempenho desses estudantes e fazendo um estudo dos distratores mais escolhidos para os itens propostos foram observadas lacunas e dificuldades no desenvolvimento das ideias características dessa temática. Todos os casos detalhados a seguir tiveram índice de acerto inferior a 50%, estando associados a tarefas como:
- Utilizar os dados de número de óbitos ao longo de uma semana, apresentados em uma tabela, para determinar a média de óbitos daquele período. Nesse caso, pouco mais de um quarto dos respondentes (25,7%) foi capaz de indicar a resposta correta, sendo que um percentual um pouco acima desse indicou a média como sendo o maior valor observado na tabela, enquanto que pouco mais de 17% associou a média com a mediana dos dados.
- Determinar a média diária do número de visitas que uma página de internet recebeu ao longo de 3 dias. Enquanto que apenas 16,3% dos respondentes executou a tarefa correta, praticamente a metade dos estudantes observou o padrão de crescimento no número de visitas que a página obteve e indicou a média aritmética como sendo o próximo número dessa suposta sequência. Além destes, 19,5% dos estudantes indicaram a soma dos números de visitas desses três dias como sendo a média.
- Obter a mediana de um conjunto de 11 números ordenados. Apenas 45% dos respondentes indicaram a alternativa correta, enquanto que quase 27% assinalaram a moda como suposta resposta correta, mostrando não terem clareza das definições das medidas de tendência central (média, mediana e moda). Os demais (28%) escolheram números inferiores a mediana, presentes no início da listagem de números.
- Resolver problema envolvendo média ponderada para determinar a média de gols por partida marcada por uma equipe na fase final de um torneio, dada a média de gols por partida na primeira fase, a média de gols por partida de todo o torneio e o número de jogos da primeira e da fase final. A alternativa mais assinalada sugere que os estudantes não relacionaram a situação descrita com ao conceito de média ponderada, mas sim ao de média simples. Para quase 30% dos respondentes, a média de gols por jogo em uma competição pode ser obtida a partir da média aritmética simples da média observada na primeira e na segunda fase da competição, mesmo essas fases tendo número de partidas diferentes. Importante destacar que o termo “média ponderada” não estava presente no enunciado, cabendo ao estudante interpretar o cenário e reconhecer a necessidade do emprego da média ponderada.
O único item associado à média aritmética que teve mais de 50% de acerto tinha como contexto o cálculo de média escolar, a partir de notas obtidas ao longo do bimestre. Esse melhor desempenho provavelmente está associado à familiaridade desse contexto com o cotidiano do respondente.
A partir das observações feitas, sugere-se ampliar os cenários investigados nas aulas de matemática, de modo a proporcionar novas experiências e vivências para o alunado, tomando maior contato com conceitos estatísticos, incluindo medidas de tendência central, em diferentes situações, contextos e cenário.
|
 |
Exemplo 2
Nível Básico
Compõe a descrição do ponto 325 da Escala de Matemática – SARESP
H33 Resolver problemas que envolvam probabilidades simples.

O item trata da resolução de um problema envolvendo a probabilidade de obter um número maior ou igual a 10 ao lançar um dado de 12 faces, enumeradas de 1 a 12. Nesse caso, ao tratar do lançamento de um único dado, o número de faces do dado corresponde ao número de elementos do espaço amostral (12), sendo que 3 dessas faces constituem o evento procurado, que é um número maior ou igual a 10, nesse caso: 10, 11 e 12. Assim, ao lançar mão da definição de clássica de probabilidade de um evento, como sendo a razão entre o número de casos favoráveis e o número total de casos possíveis, obtém-se a fração 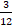 (alternativa D). (alternativa D).
Ao analisar o desempenho dos respondentes, destaca-se que a alternativa correta foi assinalada por pouco mais de um terço dos respondentes (34,8%). Ao olharmos para o grupo de menor desempenho esse índice cai para 18,1% enquanto que no grupo de maior desempenho, o percentual de acerto atinge 62,3%, de modo que, dentre aqueles 27% do alunado, que obtiveram melhor desempenho no teste, mais de um terço não conseguiu indicar a resposta correta.
É importante frisar que a tarefa proposta aborda as ideias iniciais da probabilidade, trazendo um cenário direto, cuja solução recai em reconhecer quantos números, dentre 12, são maiores ou iguais a 10. A análise dos distratores sugere que 17,3% dos respondentes possivelmente considerou que o evento procurado era um número maior do 10, ignorando a possibilidade de ser igual. Ou seja, esse grupo, juntamente com os que responderam corretamente, provavelmente sabe resolver tarefas similares a essa, porém precisam de um refinamento na leitura da descrição do cenário investigado.
Por outro lado, praticamente 10% dos estudantes indicaram  como a fração que determina a probabilidade do evento ocorrer. Essa escolha sugere que: como a fração que determina a probabilidade do evento ocorrer. Essa escolha sugere que:
- Os estudantes associaram o numerador da fração com o número 10, presente no enunciado, e não com o número de casos favoráveis;
- Esses estudantes não compreendem que indicaram uma fração que indica que o evento em questão é muito provável de ocorrer. Fato esse que possivelmente seria descartado se fosse perguntado a eles se acreditam que a chance de obter um número maior ou igual a 10 num dado de 12 faces é muito provável.
Além destes, outros 27,3% dos respondentes apontaram que a fração que determina a probabilidade de o evento ocorrer é igual a 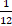 . Essa escolha possivelmente está relacionada com o seguinte trecho do enunciado: . Essa escolha possivelmente está relacionada com o seguinte trecho do enunciado:
Ela está na parte final do jogo e para ganhar ela precisa lançar o dado e tirar um número maior ou igual a 10.
Enquanto isso, os demais (10,2%) que assinalaram a fração  como alternativa de resposta, possivelmente reconheceram que há 3 números relacionados ao evento e que é necessário sortear um desses três para ganhar o jogo. O termo destacado pode ter sido a motivação para a escolha dessa alternativa de resposta. como alternativa de resposta, possivelmente reconheceram que há 3 números relacionados ao evento e que é necessário sortear um desses três para ganhar o jogo. O termo destacado pode ter sido a motivação para a escolha dessa alternativa de resposta.
Esses dois fatos sugerem que esses 37,5% dos estudantes que optaram por uma dessas alternativas, muito possivelmente, desconhecem a definição de probabilidade, apresentada anteriormente.
Outro item presente na prova que complementa o estudo de probabilidade associado ao lançamento de dados apresentava a tarefa de analisar a soma obtida a partir do lançamento de dois dados e determinar a chance de essa soma ser maior ou igual a 5, sendo acertada por apenas 20,9% dos respondentes. Cabe destacar que a análise do lançamento de dois dados de 6 faces é diferente de analisar as probabilidades referentes ao lançamento de um dado de 12 faces. Importante certificar junto aos estudantes essa percepção, uma vez que não é incomum encontrar indícios de que o espaço amostral associado ao lançamento de 2 dados é 12 (soma-se 6 de cada dado), ao invés de 36 (número correto, obtido a partir do princípio multiplicativo da contagem). Cabe lembrar que dados são objetos conhecidos pelos estudantes e que vários experimentos podem ser realizados com esses objetos a fim de aprimorar a concepção das ideias sobre probabilidade.
Em complemento, na seleção de itens que compôs a prova de matemática havia um outro item que também abordava a comparação da probabilidade de sortear uma menina e um menino numa turma, dada a quantidade de meninas e meninos nessa turma, sendo que havia mais meninas do que meninos. A partir dessa informação é possível afirmar que a probabilidade de uma menina ser sorteada é maior do que a probabilidade de um menino ser sorteado. No entanto, pouco menos de 60% dos respondentes escolheram uma alternativa condizente com essa afirmação. Apesar disso, apenas 19,3% dos estudantes conseguiram obter a resposta correta, pois além de perceber que uma probabilidade era maior do que a outra, era necessário apontar a diferença entre essas probabilidades. No enunciado desse item, a turma era composta por 22 meninas e 18 meninos, ou seja a diferença entre as probabilidades é igual 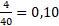 . Porém a maioria optou por indicar que a diferença era igual a 0,40, muito possivelmente por associar o número de meninas a mais (4) ao resultado informado (0,40). Por fim, ainda para esse último item, é curioso observar que aproximadamente 26% dos respondentes inverteram a situação, apontando que a probabilidade de sortear um menino seria maior do que a de sortear uma menina, enquanto que 14,4% do alunado ignorou a diferença no número de meninas e meninos, indicando que a probabilidade é a mesma para ambos. . Porém a maioria optou por indicar que a diferença era igual a 0,40, muito possivelmente por associar o número de meninas a mais (4) ao resultado informado (0,40). Por fim, ainda para esse último item, é curioso observar que aproximadamente 26% dos respondentes inverteram a situação, apontando que a probabilidade de sortear um menino seria maior do que a de sortear uma menina, enquanto que 14,4% do alunado ignorou a diferença no número de meninas e meninos, indicando que a probabilidade é a mesma para ambos.
A dificuldade observada nesses itens que abordam itens relacionados a definição usual de probabilidade sugere que os estudantes também deverão apresentar dificuldades em casos mais complexos, como aqueles que abordam união e interseção de eventos, cenários envolvendo probabilidade condicional, além de situações que associam probabilidade e análise combinatória.
|
 |
Exemplo 3
Nível Avançado
Compõe a descrição do ponto 400 da Escala de Matemática – SARESP
H30 Resolver problemas que envolvam relações métricas fundamentais (comprimentos, áreas e volumes) de sólidos, como a pirâmide e o cone.

O item aborda a resolução de um problema envolvendo o volume de pirâmide, sem contextualização, a partir das medidas de sua altura e das arestas da base, tendo a fórmula do volume como apoio. Cabe destacar que a questão não apresentava figura de apoio, cabendo ao estudante associar a pirâmide descrita com a seguinte imagem:

Vale apontar que a fórmula descrita não é exclusiva desse tipo de pirâmide, já que toda pirâmide tem seu volume como sendo igual a um terço do produto da área de sua base pela sua altura. Apesar da descrição dos elementos da fórmula presentes no enunciado da questão, boa parte dos respondentes optou por estratégias não associadas a fórmula apresentada. Algumas possíveis estratégias adotadas foram:
- Cálculo do produto da medida da aresta da base pela altura, dividido por três;
- Cálculo do produto da medida da aresta da base pela altura;
- Tentativa do cálculo de área da base multiplicado pela altura;
- Cálculo do volume de uma pirâmide, assumindo que a base é triangular.
As estratégias detalhadas anteriormente descrevem possíveis motivações para a escolha dos distratores pelos estudantes. Importante salientar que todos os distratores tiveram maior percentual de escolha do que o gabarito da questão.
No caso da alternativa (A), assinalada 24% dos candidatos, observa-se que os estudantes tomaram a medida da aresta da base como sendo a medida da área da base, obtendo 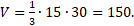 Já para a alternativa (B), a alternativa com maior percentual de escolha (37,6%), observa-se uma estratégia mais equivocada, dissociada da fórmula, na qual o resultado obtido é simplesmente o produto da medida da base pela altura. Cabe destacar, nesse caso, que os respondentes ignoraram o fato de não perceberem que esse produto acarreta num resultado dado em metros quadrados, ou seja, uma medida de área e não de volume. Para esse caso se faz necessário um acompanhamento mais de perto por parte do professorado. A alternativa (C), opção de 19,3% do alunado, possivelmente está associada a uma tentativa de cálculo de volume, porém que não faz uso da fórmula apresentada, uma vez que a solução empregada possivelmente foi o cálculo de Já para a alternativa (B), a alternativa com maior percentual de escolha (37,6%), observa-se uma estratégia mais equivocada, dissociada da fórmula, na qual o resultado obtido é simplesmente o produto da medida da base pela altura. Cabe destacar, nesse caso, que os respondentes ignoraram o fato de não perceberem que esse produto acarreta num resultado dado em metros quadrados, ou seja, uma medida de área e não de volume. Para esse caso se faz necessário um acompanhamento mais de perto por parte do professorado. A alternativa (C), opção de 19,3% do alunado, possivelmente está associada a uma tentativa de cálculo de volume, porém que não faz uso da fórmula apresentada, uma vez que a solução empregada possivelmente foi o cálculo de 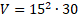 , ou seja um cálculo associado ao volume de um prisma. Além disso, também é possível que o respondente tenha feito , ou seja um cálculo associado ao volume de um prisma. Além disso, também é possível que o respondente tenha feito 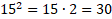 . Por fim, o último distrator, escolha de 11,5% dos respondentes, indica uma possível tentativa de uso da fórmula, porém com insucesso no cálculo da área da figura, sendo feito . Por fim, o último distrator, escolha de 11,5% dos respondentes, indica uma possível tentativa de uso da fórmula, porém com insucesso no cálculo da área da figura, sendo feito 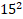 dividido por 2. dividido por 2.
A alternativa correta foi a opção de menos de 10% dos estudantes, indicando que o item foi percebido como sendo muito difícil, mesmo com o apoio de fórmula. Inclusive, os estudantes que obtiveram os melhores resultados no teste, o chamado Grupo de Maior Desempenho, teve apenas 3 pontos percentuais a mais no índice de acerto.
Em complemento à discussão apresentada, cabe trazer um segundo item relacionado a sólidos geométricos presente na prova. Detalhe importante, é que o item abordava o cálculo da altura de um cilindro, a partir de seu volume e diâmetro da base, sem o apoio de fórmula. Nesse segundo problema, que possui maior parâmetro de dificuldade, segundo a TRI, os respondentes obtiveram maior índice de acerto, sendo respondido corretamente por 26% deles. Isso pode se mostrar incoerente num primeiro instante, porém se justifica pelo fato de que o item que trazia o cilindro apresentou índice de acerto casual muito elevado.
No item que tratava da pirâmide, o índice de acerto casual é consideravelmente mais baixo, o que sugere que esse item pode ter sido melhor compreendido pelos estudantes, que buscaram resolvê-lo, ao invés de escolher uma alternativa aleatória. Contudo, ao buscarem resolver o item não fazem o uso correto das informações e fórmulas apresentadas. Isso aponta que o cenário em si foi reconhecido pelos discentes, de modo a permitir uma mobilização do conhecimento em busca da resposta correta, mas que a habilidade ainda não se mostra devidamente compreendida, a ponto de conseguirem obter a resposta correta.
|
 |
Exemplo 4
Nível Avançado
Compõe a descrição do ponto 400 da Escala de Matemática – SARESP
H06 Descrever as características fundamentais da função do 2º grau, relativas ao gráfico, crescimento, decrescimento, valores máximo ou mínimo.
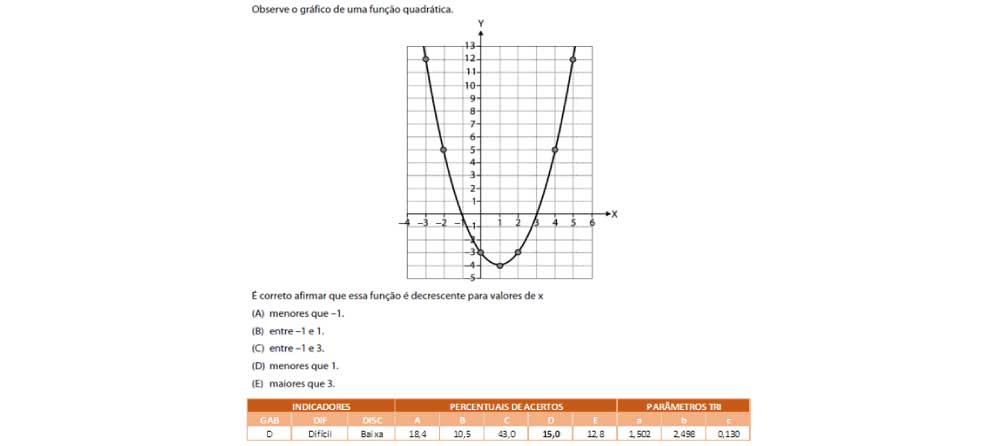
O item apresentado visa analisar o comportamento gráfico de uma função quadrática, indicando o intervalo do domínio em que a função é decrescente. A questão foi acertada por 15% dos respondentes, indicando que o item se mostrou difícil para o público avaliado. Mesmo no Grupo de Maior Desempenho esse índice de acerto não superou 20%, mostrando que a tarefa foi assimilada por poucos estudantes.
Dentre as alternativas de resposta apresentadas, destaca-se a opção (C), assinalada por quase metade (43%) dos estudantes, que traz o intervalo do domínio para o qual a função é menor do que zero. Ou seja, a alta escolha por essa alternativa muito provavelmente se deve a uma possível confusão entre ser decrescente e assumir valores negativos, já que a principal escolha dos estudantes foi pela resposta em que o intervalo de x está associado ao traço que está abaixo do eixo horizontal do plano cartesiano. Também há de se destacar que pouco mais de 18% dos estudantes escolheram a alternativa (A) como resposta, muito possivelmente por entenderem que à esquerda do –1 se tem valores negativos, numa provável e indevida associação com a reta numérica.
Cabe a investigação por parte do professorado sobre qual a dificuldade que motivou o equívoco dos estudantes que optaram por uma das alternativas incorretas. A escrita baseada no domínio da função para apresentação da resposta pode ter sido um complicador. Uma possível maneira de contornar esse dificultador é verificar junto aos estudantes se eles conseguiriam destacar no gráfico da função a parte da curva que é decrescente, sendo esperado como resposta algo como o exemplificado a seguir.
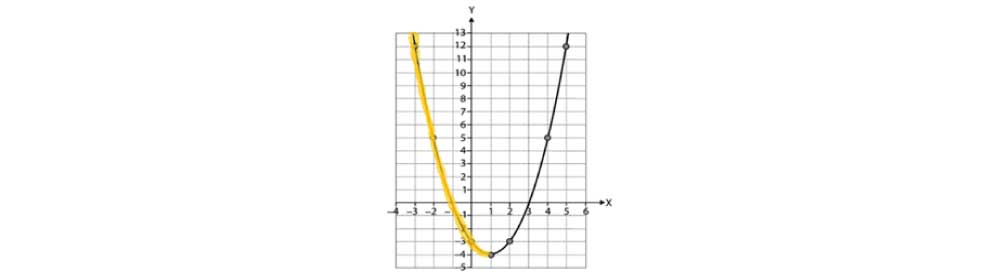
Uma vez percebido que o estudante é capaz de identificar o trecho decrescente, conforme o exemplo, a discussão pode partir para a representação desse trecho, fazendo uso da linguagem de conjuntos. Outros resultados observados ao longo do teste mostraram que a identificação de pontos específicos em um gráfico de parábola pode ser considerada uma tarefa de dificuldade mediana. Para um gráfico semelhante ao apresentado no item exemplificado, observou-se que pouco menos da metade dos respondentes conseguiram identificar o ponto de mínimo da função. Sendo alguns erros comuns indicados a seguir:
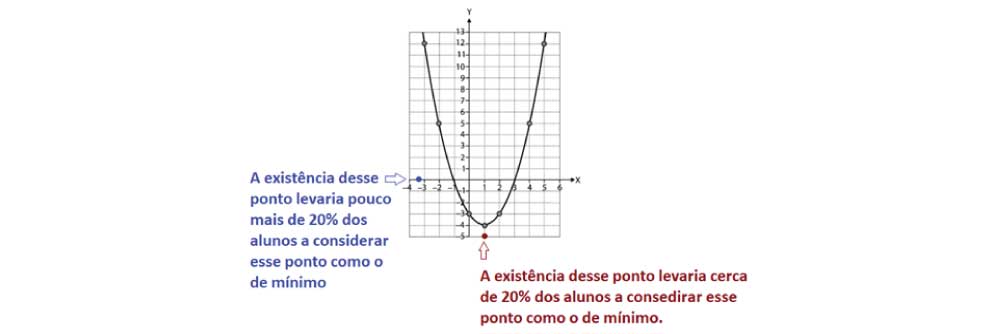
Ou seja, quase 4 em cada 10 respondentes apontaram o ponto de mínimo de uma função como sendo um ponto não pertencente a parábola, sugerindo não perceberem que pontos de uma função deverão estar contidos em seu gráfico.
Ainda sobre as características de gráficos de funções, é importante destacar, por exemplo, que pouco mais de um quarto dos respondentes conseguiu identificar a taxa de variação de uma função decrescente a partir de dois pontos destacados no gráfico, sendo conhecidas suas coordenadas. Essa tarefa foi apresentada em um item ancorado no nível Adequado na escala de proficiência.
Em suma, seja para a função de 1º ou 2º graus, a representação gráfica ainda se mostra algo distante daquilo que se entende como desejável para o ensino de matemática, de modo que os estudantes não têm conseguido mobilizar as informações contidas nesse tipo de linguagem, juntamente com suas competências cognitivas.
|
|
|
|

|
