|
 |
Introdução
As provas de Matemática são parte integrante da avaliação SARESP, estando presentes em todas as edições, ano a ano. Assim como em Língua Portuguesa, a aferição da proficiência dos estudantes em Matemática é utilizada na composição dos indicadores educacionais do Estado de São Paulo.
A partir da edição 2023, todas as turmas dos Anos Finais do Ensino Fundamental passaram a participar do SARESP, ampliando as informações coletadas. O desempenho dos estudantes de cada ano escolar está detalhado na sequência, tendo como referência a análise feita a partir da Teoria Clássica dos Testes – TCT – que toma a quantidade de acertos como referência.
Importante destacar que para a montagem das provas foi levado em consideração as habilidades previstas no Currículo Paulista, sempre priorizando aquilo que está posto para ser trabalhado ao longo dos três primeiros bimestres escolares. Por fim, é preciso lembrar que toda a aplicação ocorreu em meio digital, sendo que as questões foram apresentadas e respondidas na tela.
   
|

Considerações finais
Na sequência serão apresentados dois materiais voltados para habilidades presentes no Currículo Paulista e que os alunos do Ensino Fundamental tiveram índices de acerto mais baixos. O objetivo deste material é que o professorado de Matemática possa pensar em ações para trabalhar tais conceitos e auxiliar os estudantes em seu processo de aprendizagem de Matemática.
É claro que a avaliação e os comentários trazidos aqui não são capazes de contemplar a totalidade das diferentes realidades e recursos que cada um dos professores de Matemática têm disponível, o que enfatiza a importância da autonomia do professor para mobilizar diferentes estratégias para o ensino e aprendizagem em suas salas de aula.
Por fim, o que se objetivou com os comentários dos exercícios trazidos foi a possibilidade de tratar a avaliação como um diagnóstico, isto é, pensar em instrumentos avaliativos que possam auxiliar a identificação de dificuldades dos estudantes e, a partir desse diagnóstico, pensar em atividades que possam auxiliar os alunos a superarem-nas.
Clique nos ícones abaixo para fazer o download de cada material.
 |
|
 |


A prova do 6EF foi estruturada para avaliar os primeiros passos dos estudantes nos Anos Finais do Ensino Fundamental. Partindo do princípio que se trata de um ano de transição, que inclui muitas mudanças na rotina escolar do estudante, a seleção das questões para composição dos cadernos de provas se voltou principalmente para aferição de temas e conteúdos centrais, tanto para avaliar aquilo que era esperado que o estudante trouxesse do 5º ano, como aquilo que é objeto das aulas do 6º ano EF.
O quadro a seguir sintetiza como as questões foram percebidas pelos respondentes, tomando como referência do índice de dificuldade e o de discriminação.
DIFICULDADE
Indica o percentual de alunos que respondeu corretamente o item. Quanto maior esse índice, mais fácil foi a tarefa proposta para ele resolver.
Esse índice é dividido em 5 categorias:
Muito Fácil: percentual de acerto superior a 85%
Fácil: percentual de acerto entre 65% e 85%
Médio: percentual de acerto entre 35% e 65%
Difícil: percentual de acerto entre 15% e 35%
Muito Difícil: percentual de acerto inferior a 15%
DISCRIMINAÇÃO
Índice que analisa o percentual de acerto em dois grupos, chamados de menor e de maior desempenho, que correspondem a um recorte dos alunos da turma que realizaram a prova. O grupo de menor desempenho é constituído por aproximadamente 27% dos estudantes que obtiveram os menores escores (número de acertos) em toda a prova de matemática. Analogamente, o grupo de maior desempenho também possui contingente parecido do aluno, mas que obtiveram os maiores escores na prova. O índice de discriminação é calculado a partir da diferença do percentual de acerto desses dois grupos no item, sendo que seu propósito é comparar o desempenho desses dois grupos opostos na realização de uma determinada tarefa proposta na prova, verificando assim se o item apresentado tem a propriedade de diferenciar o desempenho daqueles que obtiveram os melhores resultados no teste daqueles que conquistaram os resultados mais tímidos. Em geral, índices de discriminação mais baixos normalmente são observados em itens extremos, ou seja, considerados muito fáceis, em que uma imensa maioria acerta, ou de itens muitos difíceis, que estão relacionados a ideias mais complexas e que se mostraram pouco consolidadas, mesmo para estudantes com bons desempenhos gerais na área de conhecimento. Em contrapartida, itens com bons índices de discriminação decorrem de tarefas cujo conhecimento necessário para sua resolução está bem consolidado no grupo de maior desempenho, mas não está para o grupo de menor desempenho.
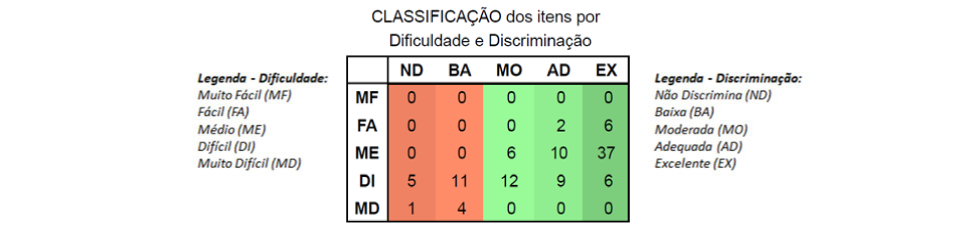
Ao analisar a porcentagem de acertos dos itens que compuseram a prova de Matemática do SARESP, vemos que apenas oito foram considerados fáceis, isto é, tiveram pelo menos 65% de acerto. Quase metade da prova teve questões consideradas de dificuldade média e, além disso, quase 40% da prova teve questões difíceis, cuja taxa de acerto do alunado foi inferior a 35%.
Ao examinar o índice de discriminação das questões, 21 apresentaram índices baixos, destacados na região alaranjada do quadro. Importante observar que todas elas foram consideradas questões difíceis ou muito difíceis, indicando que estes itens envolviam tarefas que se mostraram desafiadoras para os estudantes, inclusive para aqueles de melhor desempenho geral no teste. A saber, alguns dos conteúdos trabalhados nas questões com discriminação baixa foram:
- características de triângulos e quadriláteros quanto aos seus ângulos e medidas;
- números racionais – ordenação e representação na forma fracionária;
- razão (ideia parte-todo) representada por uma fração irredutível;
- situações-problemas que envolvem as grandezas comprimento, massa, tempo, temperatura, área (triângulos e retângulos), capacidade e volume (sólidos formados por blocos retangulares), sem uso de fórmulas;
- situações-problemas que envolvem divisão com resto;
- situações-problemas que envolvem partilha desigual.
Em contrapartida, os itens que mostraram maior taxa de acertos abordaram conteúdos normalmente vistos ao longo dos Anos Iniciais do Ensino Fundamental, dentre os quais se destacam:
- associar uma fração a uma representação pictórica;
- calcular o perímetro de retângulos com apoio de malha retangular;
- determinar a latitude e longitude de um ponto destacado em um mapa;
- identificação da posição de números racionais (em escrita decimal) na reta numérica;
- reconhecer a planificação de sólidos geométricos, com apoio da representação tridimensional do sólido;
- reconhecer padrões de sequências figurais, que envolvem a contagem de elementos.
Em geral, o que podemos notar é que recursos visuais como a reta numérica, a malha quadriculada ou representações pictóricas (como sequências figurais ou representações de frações) são elementos que favorecem um melhor desempenho do alunado.
| topo |


A prova do 7EF foi estruturada considerando os aprofundamentos dados em relação a aquilo que foi trabalhado no 6º ano. Vale lembrar que é no 7º ano que são introduzidos assuntos centrais na Matemática, como o conjunto dos números inteiros e a intensificação do uso da escrita algébrica.
O quadro a seguir sintetiza como as questões foram percebidas pelos respondentes, tomando como referência o índice de dificuldade e o de discriminação.
DIFICULDADE
Indica o percentual de alunos que respondeu corretamente o item. Quanto maior esse índice, mais fácil foi a tarefa proposta para ele resolver.
Esse índice é dividido em 5 categorias:
Muito Fácil: percentual de acerto superior a 85%
Fácil: percentual de acerto entre 65% e 85%
Médio: percentual de acerto entre 35% e 65%
Difícil: percentual de acerto entre 15% e 35%
Muito Difícil: percentual de acerto inferior a 15%
DISCRIMINAÇÃO
Índice que analisa o percentual de acerto em dois grupos, chamados de menor e de maior desempenho, que correspondem a um recorte dos alunos da turma que realizaram a prova. O grupo de menor desempenho é constituído por aproximadamente 27% dos estudantes que obtiveram os menores escores (número de acertos) em toda a prova de matemática. Analogamente, o grupo de maior desempenho também possui contingente parecido do aluno, mas que obtiveram os maiores escores na prova. O índice de discriminação é calculado a partir da diferença do percentual de acerto desses dois grupos no item, sendo que seu propósito é comparar o desempenho desses dois grupos opostos na realização de uma determinada tarefa proposta na prova, verificando assim se o item apresentado tem a propriedade de diferenciar o desempenho daqueles que obtiveram os melhores resultados no teste daqueles que conquistaram os resultados mais tímidos. Em geral, índices de discriminação mais baixos normalmente são observados em itens extremos, ou seja, considerados muito fáceis, em que uma imensa maioria acerta, ou de itens muitos difíceis, que estão relacionados a ideias mais complexas e que se mostraram pouco consolidadas, mesmo para estudantes com bons desempenhos gerais na área de conhecimento. Em contrapartida, itens com bons índices de discriminação decorrem de tarefas cujo conhecimento necessário para sua resolução está bem consolidado no grupo de maior desempenho, mas não está para o grupo de menor desempenho.
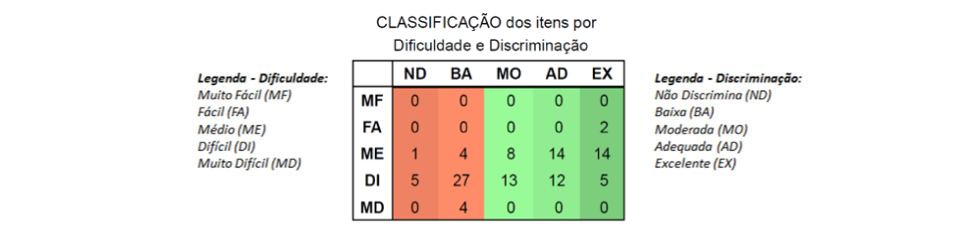
Ao analisar a porcentagem de acertos dos itens que compuseram a prova de Matemática do 7º ano EF, tem-se que apenas duas delas foram consideradas fáceis, isto é, tiveram pelo menos 65% de acerto. Esse já é um primeiro indício de que as tarefas propostas se mostraram minimamente desafiados em sua imensa maioria. Em complemento, pouco menos de 40% das questões da prova teve dificuldade considerada média e, além disso, quase 60% da prova teve questões difíceis ou muito difíceis, cuja taxa de acerto do alunado foi igual ou inferior a 35%. No geral, isso confirma a impressão inicial de que a prova de Matemática se mostrou desafiadora ao alunado.
Em outras palavras, o que o quadro mostra é que mesmo aquelas questões que abordaram temáticas centrais, consideradas introdutórias para o desenrolar de assuntos mais complexos, previstos no Currículo Paulista, não foram concebidas como fáceis pelo público avaliado.
Além disso, ao olhar para o índice de discriminação das questões, 41 delas apresentaram valores que as classificaram como ruins (região laranja do quadro), sendo que 35 foram consideradas como difíceis ou muito difíceis, indicando que provavelmente parte significativa da prova foi composta por tarefas que se mostraram desafiadoras para ampla maioria do alunado, o que inclui aqueles que obtiveram os melhores desempenho nos testes.
A saber, alguns dos conteúdos trabalhados nas questões com discriminação baixa foram:
calcular a área de trapézios;
classificar quadriláteros a partir do detalhamento de suas propriedades;
reconhecer a igualdade na medida de ângulos opostos pelo vértice;
reconhecer a translação de figuras no plano cartesiano;
resolver situações-problemas envolvendo o cálculo de frações;
resolver situações-problemas envolvendo a ideia de razão para comparar a autonomia de diferentes veículos;
utilizar simbologia algébrica para representar padrões de sequências ou para expressar relação entre o lado de um quadrado e seu perímetro ou área.
Em contrapartida, os itens que mostraram maior taxa de acertos trabalharam conteúdos como:
calcular a probabilidade de evento simples, que resulta em 1/n;
ordenar números racionais em um contexto de alturas de pessoas;
reconhecer a figura resultante de uma rotação de 90° em torno de um ponto ou de uma reflexão em relação ao eixo x;
resolver situação-problema envolvendo números inteiros (positivos e negativos entre -10 e +10) para calcular o total de pontos em um jogo;
resolver situações-problemas envolvendo porcentagem (50%);
resolver situações-problemas envolvendo proporção simples.
Vale destacar que, nas situações problemas com porcentagem e proporção citadas, o contexto envolvia a compra de produtos, em que o alunado mostrou certa afinidade com a contextualização trazida.
Por fim, parte dos itens utilizados na composição da prova do 7º ano EF eram questões comuns às da prova do 6º ano EF. Ao olharmos para as estatísticas dos itens comuns entre esses dois anos escolares, nota-se que o alunado do 7° ano teve um percentual de acertos maior ou igual em relação aos estudantes do 6° ano. Em apenas duas questões dos 45 itens comuns, vimos que os estudantes da série mais nova tiveram um percentual de acerto consideravelmente maior (cerca de 4 pontos percentuais). Vale lembrar que esse é o comportamento esperado, no qual os estudantes com maior tempo de escolaridade se mostram mais aptos na resolução de problemas, quando comparados aos estudantes com trajetória escolar mais curta.
Ao olharmos para as duas questões indicadas, vemos que entre os conteúdos trabalhados nelas estavam a soma de frações com denominadores diferentes e o cálculo de probabilidade de um evento aleatório. Uma possível explicação para o melhor desempenho dos estudantes do 6° ano é considerar que as habilidades dessas duas questões estão previstas, segundo o Currículo Paulista, para serem trabalhadas no próprio 6° ano, o que indica que eles teriam visto tal conteúdo de forma mais recente quando comparados com os estudantes do 7° ano.
Assim sendo, assuntos relacionados a essas duas tarefas podem ser revistos junto ao professorado do 7º ano EF, de modo que sejam pensadas em retomadas ao longo do ano escolar, associadas a aulas que dialoguem com essa temática, favorecendo a continuidade dos tópicos estudados no ano anterior. O ato de revisitar permite que o estudante ressignifique algumas de suas ideias, corrigindo aquilo que for necessário, além de aperfeiçoar ideias ainda em fase de consolidação.
| topo |


A prova do 8º ano EF foi estruturada com enfoque na continuidade de algumas temáticas iniciadas no 7º ano. Inclusive, parte da prova do 8EF foi composta por um bloco de questões presentes na prova do 7EF, com a finalidade de se verificar como se deu a apropriação de determinados assuntos e habilidades com o desenrolar dos anos, assim como o aprofundamento deles.
Além disso, a prova também se voltou para a aferição de tópicos relevantes para outros componentes curriculares, como é o caso da introdução à notação científica, de uso recorrente nas Ciências da Natureza, e de gráficos, que costumam ser utilizados tanto em Ciências da Natureza como em Ciências Humanas, por exemplo.
O quadro a seguir sintetiza como as questões foram percebidas pelos respondentes, tomando como referência o índice de dificuldade e o de discriminação.
DIFICULDADE
Indica o percentual de alunos que respondeu corretamente o item. Quanto maior esse índice, mais fácil foi a tarefa proposta para ele resolver.
Esse índice é dividido em 5 categorias:
Muito Fácil: percentual de acerto superior a 85%
Fácil: percentual de acerto entre 65% e 85%
Médio: percentual de acerto entre 35% e 65%
Difícil: percentual de acerto entre 15% e 35%
Muito Difícil: percentual de acerto inferior a 15%
DISCRIMINAÇÃO
Índice que analisa o percentual de acerto em dois grupos, chamados de menor e de maior desempenho, que correspondem a um recorte dos alunos da turma que realizaram a prova. O grupo de menor desempenho é constituído por aproximadamente 27% dos estudantes que obtiveram os menores escores (número de acertos) em toda a prova de matemática. Analogamente, o grupo de maior desempenho também possui contingente parecido do aluno, mas que obtiveram os maiores escores na prova. O índice de discriminação é calculado a partir da diferença do percentual de acerto desses dois grupos no item, sendo que seu propósito é comparar o desempenho desses dois grupos opostos na realização de uma determinada tarefa proposta na prova, verificando assim se o item apresentado tem a propriedade de diferenciar o desempenho daqueles que obtiveram os melhores resultados no teste daqueles que conquistaram os resultados mais tímidos. Em geral, índices de discriminação mais baixos normalmente são observados em itens extremos, ou seja, considerados muito fáceis, em que uma imensa maioria acerta, ou de itens muitos difíceis, que estão relacionados a ideias mais complexas e que se mostraram pouco consolidadas, mesmo para estudantes com bons desempenhos gerais na área de conhecimento. Em contrapartida, itens com bons índices de discriminação decorrem de tarefas cujo conhecimento necessário para sua resolução está bem consolidado no grupo de maior desempenho, mas não está para o grupo de menor desempenho.
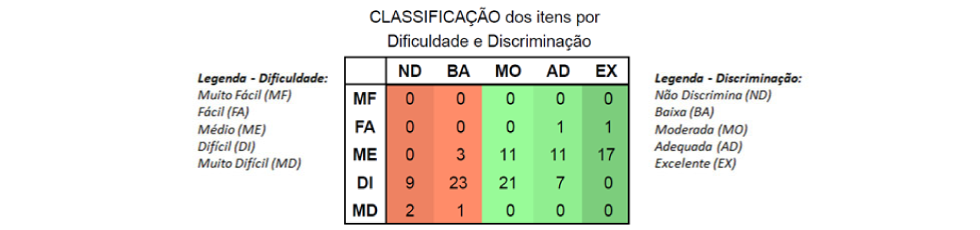
Ao analisar a porcentagem de acertos dos itens que compuseram a prova de Matemática do 8EF, vemos que apenas duas delas foram consideradas fáceis, isto é, tiveram pelo menos 65% de acerto. Ou seja, novamente, um número ínfimo de questões se mostrou simples para o alunado. Aliás, até aqui, com o transcorrer dos anos escolares avaliados, a prova de Matemática foi sendo percebida como mais difícil.
Dando continuidade, cerca de 38% das questões da prova tiveram dificuldade considerada média e, além disso, quase 60% da prova teve questões difíceis ou muito difíceis, cuja taxa de acerto do alunado foi igual ou inferior a 35%. No geral, pode-se afirmar que a prova de Matemática se mostrou desafiadora ao alunado, em especial para cerca de um terço das tarefas propostas nos cadernos de prova, uma vez que mesmo os alunos com os melhores resultados gerais não tiveram um desempenho que mereça destaque nesses casos.
Ao nos debruçarmos sobre o índice de discriminação das questões, percebemos que 38 questões tiveram discriminação ruim (região laranja do quadro). A saber, algumas das habilidades trabalhadas e que se mostraram complexas para o alunado do 8° ano foram:
associar a expressão algébrica à sua representação gráfica;
calcular porcentagens consecutivas (porcentagem de porcentagem);
classificar quadriláteros a partir do detalhamento de suas propriedades;
fazer uso da escrita algébrica para representar padrões de sequências;
identificar a posição de frações na reta numérica, tendo números em escrita decimal como referência;
identificar características dos quadriláteros, classificá-los em relação a lados e a ângulos e reconhecer a inclusão e a intersecção de classes entre eles.
reconhecer a equação de uma função do primeiro grau a partir da apresentação do gráfico;
resolver problemas envolvendo o cálculo de volume de blocos retangulares.
Em contrapartida, os itens que mostraram maior taxa de acertos trabalharam conteúdos como:
realizar operações simples do campo aditivo e multiplicativo com números inteiros e números racionais em situações-problemas envolvendo o sistema monetário brasileiro;
interpretar dados presentes em tabelas de frequências e gráficos de colunas, bem como identificar dos gráficos que representa os dados fornecidos por uma tabela de frequências;
identificar padrões simples de sequências como progressões aritméticas de razão inteira.
resolver situação-problema envolvendo números inteiros (positivos e negativos entre -10 e +10) para calcular o total de pontos em um jogo;
resolver situação-problema envolvendo proporção direta simples.
Por fim, parte dos itens utilizados na composição da prova do 8º ano EF eram questões comuns a prova do 7º ano EF. Ao olharmos para as estatísticas dos itens comuns entre o 7° e o 8° do Ensino Fundamental, nota-se que o alunado do 8° ano teve um percentual de acertos maior ou igual em relação aos estudantes do 7° ano. Em apenas três questões dos 45 itens comuns, vimos que os estudantes da série mais nova tiveram um percentual de acerto consideravelmente maior (pouco menos de 4 pontos percentuais em duas delas e 6,5 pontos percentuais na outra). Conforme apontado na análise do 7EF, esse é o comportamento esperado, no qual os estudantes com maior tempo de escolaridade se mostram mais aptos na resolução de problemas, quando comparados aos estudantes com trajetória escolar mais curta.
Nas questões em que os estudantes do 7° ano tiveram quase 4 pontos percentuais de acerto a mais, os conteúdos dos itens estavam relacionados ao uso de simbologia algébrica para indicar o termo geral de elementos de uma sequência e à verificação que a soma das medidas dos ângulos internos de um triângulo é 180° para a resolução de um problema que apresentava dois dos três ângulos internos de um triângulo. Já a questão que apresentou 6,5 pontos percentuais tratava da ordenação de números racionais em uma reta numérica em que tínhamos tanto números escritos na forma decimal quanto na forma fracionária.
No caso da questão que aborda o uso da simbologia algébrica, vale destacar que o assunto é formalizado ao longo do 7º ano EF. Desse modo, é esperado que o assunto seja tratado de modo mais enfático, propiciando maior contato com tarefas relacionadas à temática, o que pode favorecer retomadas mais constantes perante as dificuldades observadas, o que pode levar a redução de erros.
Os demais assuntos (propriedade da soma dos ângulos internos e ordenação de racionais apresentados em diferentes representações) são conhecidos desde o 6º ano EF. O maior percentual de erro observado no 8EF pode se justificar pela internalização de ideias e concepções errôneas atreladas a essas temáticas. Quando não são corrigidos, os equívocos vão se internalizando, passando a ser considerados como verdades por parte dos estudantes. Um exemplo disso é a afirmação de que a fração 1/5 é equivalente ao decimal 1,5, visto que ambos fazem uso dos mesmos algarismos em sua escrita.
A perpetuação do erro é algo que precisa ser prontamente corrigida pelos professores que atuam na rede pública, independentemente do ano em que atuam, e do fato de que o erro decorre de ideias mal-formadas, advindas de discussões dos anos anteriores. Desconstruir ideias equivocadas deve ser uma prática recorrente do professorado, a fim de evitar a consolidação indevida de certas convicções que não têm respaldo no conhecimento formal daquele componente curricular.
| topo |


Primeira formalização do conceito de função, tanto de 1º como de 2º grau, além de tópicos específicos que envolvem temas da Geometria e de Grandezas e Medidas – Relações métricas no triângulo retângulo, teorema de Pitágoras e teorema de Tales. O Currículo também prevê situações mais complexas sendo trabalhadas no campo na probabilidade.
O quadro a seguir sintetiza como as questões foram percebidas pelos respondentes, tomando como referência o índice de dificuldade e o de discriminação.
DIFICULDADE
Indica o percentual de alunos que respondeu corretamente o item. Quanto maior esse índice, mais fácil foi a tarefa proposta para ele resolver.
Esse índice é dividido em 5 categorias:
Muito Fácil: percentual de acerto superior a 85%
Fácil: percentual de acerto entre 65% e 85%
Médio: percentual de acerto entre 35% e 65%
Difícil: percentual de acerto entre 15% e 35%
Muito Difícil: percentual de acerto inferior a 15%
DISCRIMINAÇÃO
Índice que analisa o percentual de acerto em dois grupos, chamados de menor e de maior desempenho, que correspondem a um recorte dos alunos da turma que realizaram a prova. O grupo de menor desempenho é constituído por aproximadamente 27% dos estudantes que obtiveram os menores escores (número de acertos) em toda a prova de matemática. Analogamente, o grupo de maior desempenho também possui contingente parecido do aluno, mas que obtiveram os maiores escores na prova. O índice de discriminação é calculado a partir da diferença do percentual de acerto desses dois grupos no item, sendo que seu propósito é comparar o desempenho desses dois grupos opostos na realização de uma determinada tarefa proposta na prova, verificando assim se o item apresentado tem a propriedade de diferenciar o desempenho daqueles que obtiveram os melhores resultados no teste daqueles que conquistaram os resultados mais tímidos. Em geral, índices de discriminação mais baixos normalmente são observados em itens extremos, ou seja, considerados muito fáceis, em que uma imensa maioria acerta, ou de itens muitos difíceis, que estão relacionados a ideias mais complexas e que se mostraram pouco consolidadas, mesmo para estudantes com bons desempenhos gerais na área de conhecimento. Em contrapartida, itens com bons índices de discriminação decorrem de tarefas cujo conhecimento necessário para sua resolução está bem consolidado no grupo de maior desempenho, mas não está para o grupo de menor desempenho.
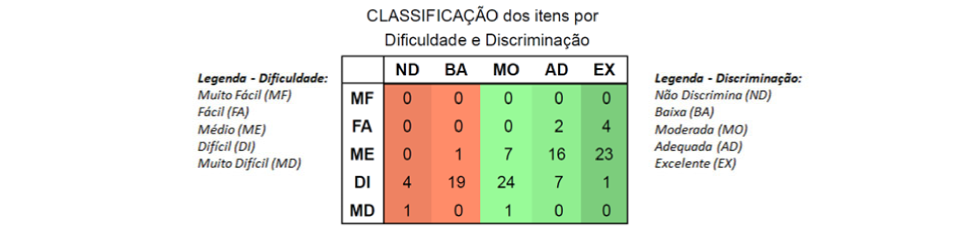
Ao analisar a porcentagem de acertos dos 110 itens que compuseram a prova de Matemática do SARESP do 9° ano, vemos que apenas seis delas foram consideradas fáceis, isto é, tiveram pelo menos 65% de acerto. Cerca de 43% das questões da prova tiveram dificuldade considerada média e, além disso, quase cerca de metade das questões da prova teve dificuldade considerada difícil ou muito difícil, cuja taxa de acerto do alunado foi igual ou inferior a 35%. No geral, podemos ver que a prova de Matemática se mostrou desafiadora ao alunado.
Ao examinar o índice de discriminação das questões, 25 questões tiveram discriminação baixa. Destas 24 questões, 23 foram consideradas com grau de dificuldade difícil ou muito difícil, indicando que provavelmente estes itens envolviam habilidades que foram desafiadoras para os estudantes.
A saber, algumas das habilidades trabalhadas e que se mostraram complexas para o alunado do 9° ano foram:
calcular a densidade demográfica;
identificar características de casos que garantem a semelhança de triângulos;
modelar situações-problemas por meio de sistemas lineares com duas incógnitas;
reconhecer a expressão algébrica que determina uma área retangular destacada (produto notável);
reconhecer gráficos de funções do 1° e do 2° a partir de suas equações algébricas.
resolver problemas envolvendo o cálculo de números escritos em notação científica;
resolver problemas característicos envolvendo o Teorema de Tales;
resolver problema envolvendo grandezas inversamente proporcionais;
resolver problemas envolvendo relações métricas no triângulo retângulo.
Em contrapartida, os itens que mostraram maior taxa de acertos trabalharam conteúdos como:
calcular a média aritmética simples de quatro notas, em um contexto que remete ao cotidiano escolar;
interpretar os dados apresentados em diferentes tipos de gráficos (barras, setores) e tabelas de frequência;
identificar os gráficos que representam os dados fornecidos por uma tabela de frequências ou um excerto;
reconhecer as coordenadas de um ponto no plano cartesiano, tendo outros pontos como referência;
reconhecer triângulos semelhantes a partir da relação de proporcionalidade entre as medidas dos lados que os formam;
resolver problemas envolvendo partições não iguais (um valor é o triplo do outro)
resolver situações-problemas envolvendo operações elementares com números naturais;
resolver situações-problemas envolvendo proporcionalidade direta simples.
| topo |
|
 |
|

|
| |
|
|