|
 |
Nova forma de acesso ao Ensino Superior, o Provão Paulista consiste em um processo seletivo seriado, voltado para os alunos da 1ª, 2ª e 3ª séries do Ensino Médio, integrado ao projeto do SARESP. Trata-se de provas formuladas com questões de múltipla escolha, que abordam tópicos do currículo paulista das séries avaliadas. Além disso, para os alunos da 3ª série, também é prevista a produção de um texto dissertativo-argumentativo.
Para as três séries avaliadas, a composição da prova da edição 2023 foi a seguinte:
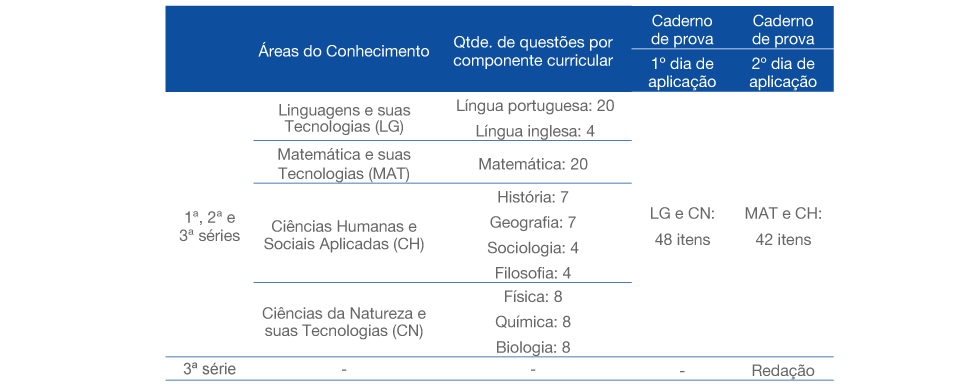
As provas ocorreram em dias letivos e, como era composta de dois cadernos distintos a serem aplicados em dois dias, a prova da 3ª série teve sua aplicação nos dias 30 de novembro e 1º de dezembro e, para a 1ª e 2ª série, a aplicação ocorreu nos dias 04 e 05 de dezembro, seguindo parte do rito já conhecido do SARESP. O Provão Paulista, em sua primeira edição, foi aplicado para 1 145 672 estudantes, sendo a grande maioria desses provenientes da rede estadual. Os índices de presença dos estudantes da rede estadual estão detalhados na sequência.
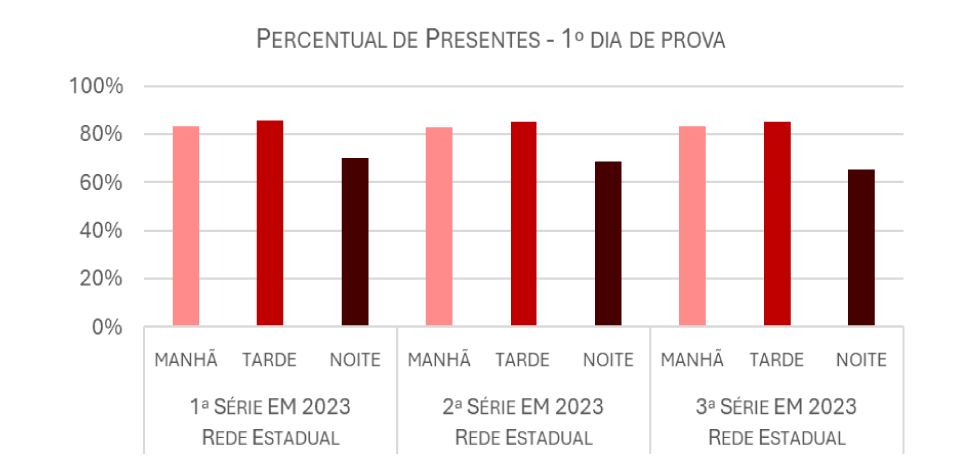
Como se nota, a participação dos alunos do período noturno foi inferior à participação dos alunos dos demais períodos para as três séries. É provável que isso esteja vinculado ao período de aplicação das provas ter sido diferente daquele em que ocorrem as aulas, o que exigiu uma mobilização diferente por parte dos estudantes do período noturno para participarem do exame.
O desempenho dos estudantes da rede estadual em cada um dos componentes curriculares, organizados por dia de aplicação, pode ser conferido na tabela a seguir. Os dados mostram os resultados obtidos pelos estudantes paulistas nas provas de cada uma das séries avaliadas:
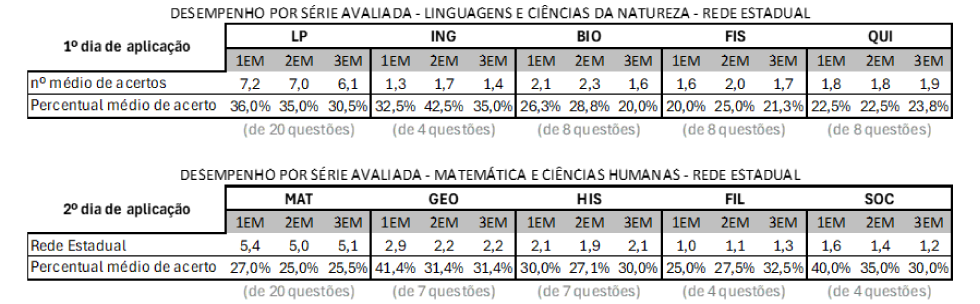
De modo geral, para a área de Linguagem e Ciências Humanas, os alunos foram capazes de acertar, em média, entre 30% e 40% da prova, indicando que as provas se mostraram com um nível de dificuldade de mediano para difícil. Já para Matemática e Ciências da Natureza, os acertos ficaram compreendidos entre 20% e 30%, sinalizando provas percebidas como difíceis.
Para a 3ª série EM, a prova também contemplava uma proposta de redação dissertativa-argumentativa. Contudo, a correção da produção escrita dos estudantes estava atrelada ao cumprimento de duas condições. São elas:
-
Acertar mais de 22 questões, dentre as 90 propostas;
-
Acertar pelo menos uma questão de cada componente curricular.
Dessas condições, a segunda foi a que impediu maior contingente de alunos de ter sua redação corrigida. A tabela a seguir mostra o número de alunos, e o respectivo percentual, que não acertou uma questão para cada componente curricular:
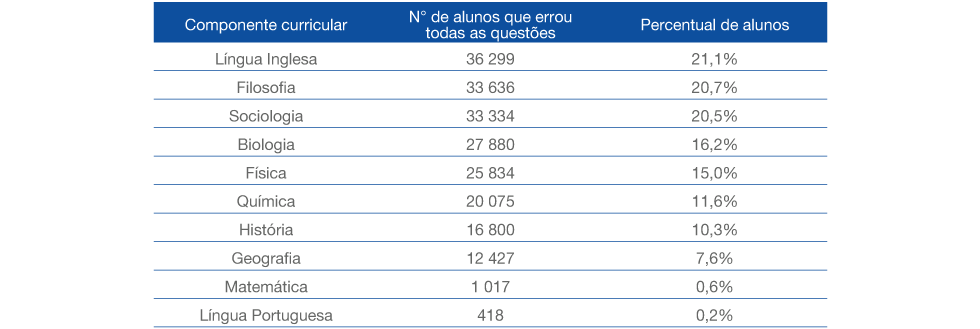
Os dados foram organizados de modo decrescente, de modo que, ao analisar os dados da tabela de cima para baixo, é possível observar em quais componentes curriculares houve maior contingente de estudantes que não conseguiram assinalar a resposta correta para ao menos uma questão presente no Provão. É importante observar que os três primeiros componentes dessa lista são aqueles com menor número de questões presentes no teste, apenas 4.
Assim sendo, quase 50 mil estudantes tiveram suas redações corrigidas. A maior parte das notas atribuídas às redações desse grupo de alunos variou de 6 a 8 pontos, numa pontuação de 0 a 10, conforme mostra o histograma:
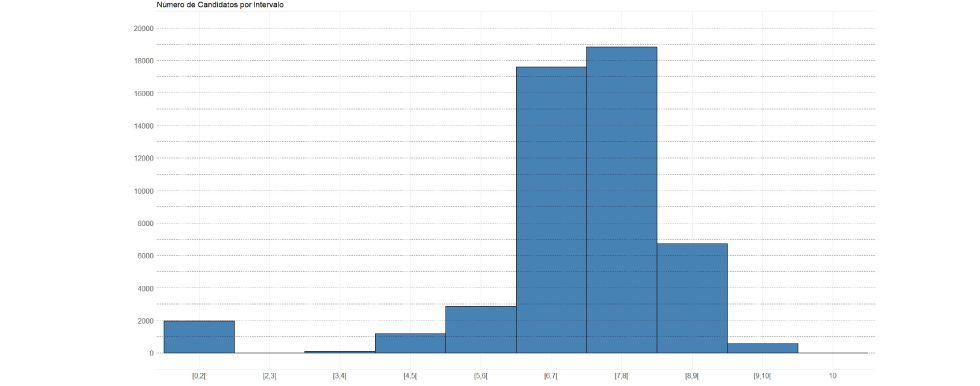
Nessa aplicação do Provão, os estudantes que tiveram suas produções textuais corrigidas atingiram bons resultados gerais, com sua nota final variando de 6 a 8, sendo 10 a nota máxima possível. Os dois critérios que se mostraram mais difíceis para os estudantes e, consequentemente, tiveram maior responsabilidade pela queda da nota foram os critérios de "Registro/norma-padrão" e de "Proposta de intervenção".
Importante destacar que a nota zero foi atribuída em casos específicos, divulgados em Edital.
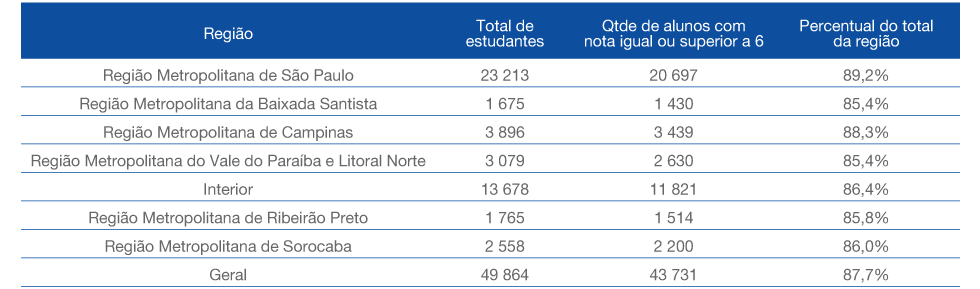
Na sequência, a tabela mostra a região de origem dos estudantes que tiveram suas redações corrigidas e quantos deles obtiveram nota 6 ou mais.
Por fim, seguem dois arquivos, um voltado para os professores de Língua Portuguesa e outro para os de Matemática. Esses materiais discutem o desempenho dos estudantes em questões que abordam habilidades centrais desses componentes curriculares e que, em anos anteriores, eram encontrados nas provas do SARESP. A proposta desse material complementar é trazer inferências sobre a evolução da aprendizagem no Ensino Médio, traçando paralelos entre o Provão Paulista e as provas realizadas até 2022 pelo SARESP, buscando correlações entre temáticas específicas desses componentes curriculares.
Clique no ícone abaixo para fazer acessar o material preparado.

Medidas Centrais – um breve estudo
O objetivo do presente material é analisar o desempenho dos estudantes no Provão Paulista no que tange ao conteúdo Medidas Centrais, na temática Estatística. As questões selecionadas têm formato similar ao observado em edições anteriores do SARESP, de modo que a discussão aqui apresentada visa inferir correlações sobre os desempenhos dos estudantes nessas diferentes provas. Além disso, a escolha da temática se justifica por possibilitar um trabalho em sala voltado a situações do cotidiano e, assim, servir de estímulo para o alunado. Essa interlocução com o que ocorre para além dos muros da escola é tida como essencial, como destaca a Nova Base Comum Curricular (BNCC), sobretudo quando promove o diálogo entre os saberes matemáticos e as experiências e conhecimentos matemáticos já vivenciados pelos alunos.
Isso aparece de modo enfático no Currículo Paulista que cita a possibilidade de o professorado fazer uso da extensa quantidade de informações divulgadas pela mídia, jornais e redes de comunicação, muitas vezes sob a forma de tabelas e gráficos, para desenvolver o trabalho com medidas centrais, o que exige dos estudantes a capacidade de leitura e interpretação desses dados.
Logo, o desenvolvimento dessa temática nas aulas de matemática pode se valer de diferentes informações associadas ao cotidiano dos estudantes, bem como de contextos variados, como o scouts de partidas ou campeonatos esportivos; dados sobre acessos divulgados por aplicativos de vídeo e música; histórico de eventos climáticos de determinado local ou região – média de chuvas ou temperatura; rentabilidade média de uma aplicação financeira, entre outras opções.
Muitas vezes, a discussão pode partir de algo ainda mais próximo do cotidiano estudantil, como o cálculo das médias bimestrais escolares. No entanto, é necessário que o alunado desenvolva
[...] a capacidade de abstrair o contexto, apreendendo relações e significados, para aplicá-los em outros contextos. Para favorecer essa abstração, é importante que os alunos reelaborem os problemas propostos após os terem resolvido. [...] Assim, pretende-se que os alunos formulem novos problemas, baseando-se na reflexão e no questionamento sobre o que ocorreria se alguma condição fosse modificada ou se algum dado fosse acrescentado ou retirado do problema proposto. (BNCC – p.299)
O histórico escolar dos alunos quanto à temática Medidas Centrais se inicia no 7º ano do Ensino Fundamental, perpassando por todos os anos seguintes, inclusive o Ensino Médio. Ao analisarmos o Currículo Paulista, temos as seguintes habilidades elencadas:
(EF07MA35) Compreender, em contextos significativos, o significado de média estatística como indicador da tendência de uma pesquisa, calcular seu valor e relacioná-lo, intuitivamente, com a amplitude do conjunto de dados.
(EF08MA25) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.
(EF09MA23) Planejar e executar pesquisa amostral envolvendo tema da realidade social e comunicar os resultados por meio de relatório contendo avaliação de medidas de tendência central e da amplitude, tabelas e gráficos adequados, construídos com o apoio de planilhas eletrônicas.
(EM13MAT202) Planejar e executar pesquisa amostral sobre questões relevantes, usando dados coletados diretamente ou em diferentes fontes, e comunicar os resultados por meio de relatório contendo gráficos e interpretação das medidas de tendência central e das medidas de dispersão (amplitude e desvio padrão), utilizando ou não recursos tecnológicos.
(EM13MAT316) Resolver e elaborar problemas, em diferentes contextos, que envolvem cálculo e interpretação das medidas de tendência central (média, moda, mediana) e das medidas de dispersão (amplitude, variância e desvio padrão).
De posse desse rol de habilidades, é válida, portanto, a expectativa de que o ingressante no Ensino Médio paulista tenha vivenciado experiências variadas com a temática em discussão ao longo do Ensino Fundamental, inclusive a partir da realização de pesquisas, levantamentos e análises de dados. De maneira direta, pode-se então afirmar que a temática não deve ser tomada como novidade para esse público. Entretanto, isso contrasta com o resultado obtido para uma questão proposta aos estudantes da 1ª série do EM no Provão Paulista.
Figura 1 – Provão Paulista – 1ª série EM

Questão com perfil de problema de fixação, comumente trabalhado nas aulas de Matemática, com a finalidade de aferir a capacidade de os alunos calcularem medidas centrais, a partir da obtenção da média, mediana e moda para um mesmo conjunto de dados.
Para essa questão, em particular, a maneira mais simples de obter a resposta correta é analisar a moda e a média do conjunto formado por 11 elementos. Nesse caso, a moda é 22 porque é o valor que mais se repete; o que faz com que as possibilidades de resposta correta se limitem a (B) ou (E). Dado que a média, para esse caso, é um valor necessariamente entre 15 e 28, a alternativa (E) passa a ser uma resposta impossível, permitindo, assim, ao estudante concluir que a resposta correta é (B), mesmo sem ter calculado efetivamente o valor da média e da mediana.
No caso de o respondente querer calcular a mediana, é importante destacar que os dados já estão organizados e ordenados, de modo que basta localizar o valor central para obtenção dessa medida, uma vez que o número de elementos do conjunto é ímpar.
Em resumo, tem-se:

Para essa questão, o índice de acerto foi de 27,1%, indicando que a grande maioria dos respondentes não foi capaz de identificar a resposta correta. Vale destacar que as alternativas (B) e (C) são similares, tendo como diferença a inversão dos valores de mediana e de moda. Contudo, as demais alternativas de resposta apresentam resultados absurdos em relação ao conjunto de dados, como:
-
Tomar a média como sendo um valor superior ao maior número presente no conjunto;
-
Tomar a moda como sendo um número que não está listado no conjunto de dados.
Esses dados sugerem que a temática Medidas Centrais ainda se mostra pouco familiar aos estudantes ingressantes no Ensino Médio, embora sejam habilidades previstas para os Anos Finais do Ensino Fundamental, segundo o Currículo Paulista. Logo, parece ser crucial aos professores da rede estadual retomar o referido conteúdo ao iniciar o trabalho com essa temática junto ao alunado.
Em complemento, para o Ensino Médio, observa-se que as duas habilidades específicas desse ciclo (EM13MAT202 e EM13MAT316) são objeto de estudo nas três séries, voltando à temática, seja para a realização de pesquisas, seja para a resolução de problemas em diferentes contextos. Sobre esse segundo aspecto, é de extrema relevância a abordagem de diferentes contextos, uma vez que os resultados das últimas edições do SARESP sugerem que tarefas relacionadas ao cálculo da média escolar são consideradas mais simples no que tange às medidas centrais, sendo normalmente ancoradas no nível Básico, tanto para o 9º ano EF como para a 3ª série EM.
A seguir, são apresentados dois exemplos envolvendo essa contextualização e seus resultados.
Figura 2 – SARESP 2022 – 9º ano EF

Tema central: média aritmética simples.
Percentual de acerto: 53,6%
Observação: questão que aborda um cenário muito familiar para os estudantes e com baixo número de elementos envolvidos (4 notas), criando condições favoráveis para a obtenção da resposta. Mesmo assim, praticamente metade dos estudantes não assinalou a resposta correta, sendo que parte considerável (cerca de 21%) optou pela alternativa (D), que corresponde à média das provas 2 e 3; o que sugere uma confusão entre os conceitos de média e mediana (que tomou a ordenação das provas, em vez das notas, como referência).
Figura 3 – SARESP 2021 – 3ª série EM
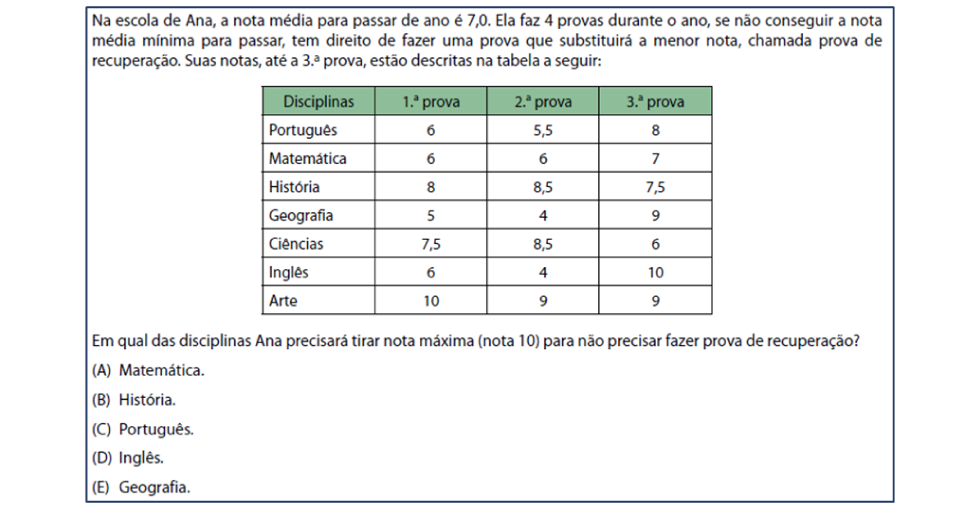
Tema central: média aritmética simples.
Percentual de acerto: 60,6%
Observação: é provável que a experiência de analisar o próprio boletim favoreça os estudantes na obtenção da resposta correta, sendo pouco crível que tenham recorrido à modelagem de uma inequação para concluírem qual a alternativa de resposta. É mais provável que eles tenham verificado a situação de cada disciplina, identificando aquela com menor somatório para os três primeiros bimestres. Além disso, vale ressaltar que os dados apresentados permitem o teste das alternativas, ou seja, era possível atribuir nota 10 para a 4ª prova de cada disciplina elencada nas alternativas e, em seguida, calcular a média.
Esses resultados sugerem que a temática Medidas Centrais não pode ser considerada como desconhecida para o público da rede estadual. Entretanto, ela parece estar fortemente associada ao contexto de notas e cálculo de média de provas, haja vista o baixo desempenho dos alunos da 3ª série EM no Provão Paulista, observado na questão a seguir.
Figura 4 – Provão Paulista – 3ª série EM

Nota-se que o problema explora unicamente a ideia de média aritmética simples, de modo que a resposta é obtida a partir da soma dos quatro valores apresentados, seguida da divisão do resultado obtido por 4. Nesse caso, a opção correta é 235 reais, alternativa (E), assinalada por 43,3% do alunado, percentual inferior ao observado nos dois exemplos citados anteriormente, presentes em edições passadas do SARESP. Se considerarmos a questão de Ensino Médio, a redução no percentual de acerto é de aproximadamente 17 pontos percentuais.
Claro, há de se considerar os possíveis impactos causados pela mudança das provas habituais do SARESP para as do Provão Paulista, novidade para o público avaliado, os quais podem ter interferido no desempenho do alunado do Ensino Médio na questão destacada.
Dados anteriores, que tomam apenas o SARESP como parâmetro, também reforçam essa suspeita de que a mudança de contexto caracteriza um dificultador para o público em questão. O exemplo a seguir foi proposto na edição 2022 do SARESP.
Figura 5 – SARESP 2022 – 3ª série EM
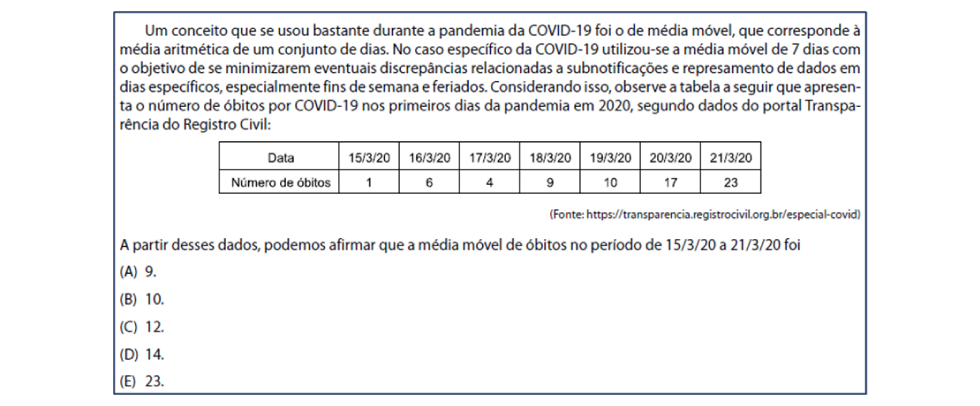
Novamente, a temática envolvida é a de média aritmética simples, porém num contexto de média de óbitos, assunto recorrente nos noticiários durante a pandemia da Covid-19. Há um complicador que é o aumento no número de dados envolvidos no cálculo, exigindo a divisão por 7 após o somatório. Contudo, há de se questionar se isso justifica a queda acentuada no desempenho dos estudantes, uma vez que o percentual de acerto foi de aproximadamente 28%, apenas.
A alternativa (E), distrator mais assinalado, sugere que os alunos optaram pelo maior valor como resposta, levantando dúvidas a respeito do entendimento desses sobre o conceito de média móvel, presente no enunciado, claramente associado ao conceito de média aritmética. Em complemento, a alternativa (A) foi a segunda opção incorreta mais assinalada e corresponde ao dado central da tabela, ideia relacionada ao conceito de mediana, indicando possível confusão entre as definições das medidas centrais.
Assim, até o momento, são dois os pontos centrais da discussão:
i) uma possível falta de clareza entre as definições das medidas centrais, tanto para os alunos do Ensino Fundamental, quando a temática está em seu desenrolar inicial e voltada à fixação das ideias, quanto para os do Ensino Médio, cuja proposta é a de diversificação de situações e aprofundamento na resolução de diferentes situações-problemas;
ii) uma provável dificuldade em extrapolar para contextos que fogem ao cálculo da média aritmética de notas escolares, ou seja, de abstrair ideias já internalizadas pela maioria dos estudantes em um contexto familiar para outros.
Em vista dos apontamentos feitos, propomos uma pausa na discussão sobre o desempenho dos estudantes no que tange ao conceito de média aritmética simples para abordar as demais medidas centrais previstas no currículo. O conceito de moda estatística é relativamente direto e simples, o acerto ou o erro na obtenção dessa medida recai sobre o estudante se dispor a analisar a situação proposta, bem como a capacidade de recordar a definição do conceito para a obtenção da resposta. Essa necessidade de relembrar as definições se deve principalmente ao fato de considerarmos que, em avaliações e processos seletivos, o aluno não pode fazer uso de tecnologias de apoio, como calculadora ou planilhas eletrônicas. Assumindo-se isso, a discussão se volta para o conceito de mediana.
Um aspecto muito importante para o professorado estar atento é a necessidade de explorar diferentes recursos para a exposição dos dados coletados, fazendo uso não somente de listagens e tabelas, mas também de gráficos. A questão apresentada na sequência também contém elementos que são dificultadores para os estudantes, ao resolverem problemas envolvendo o assunto.
Figura 6 – Provão Paulista – 3ª série EM
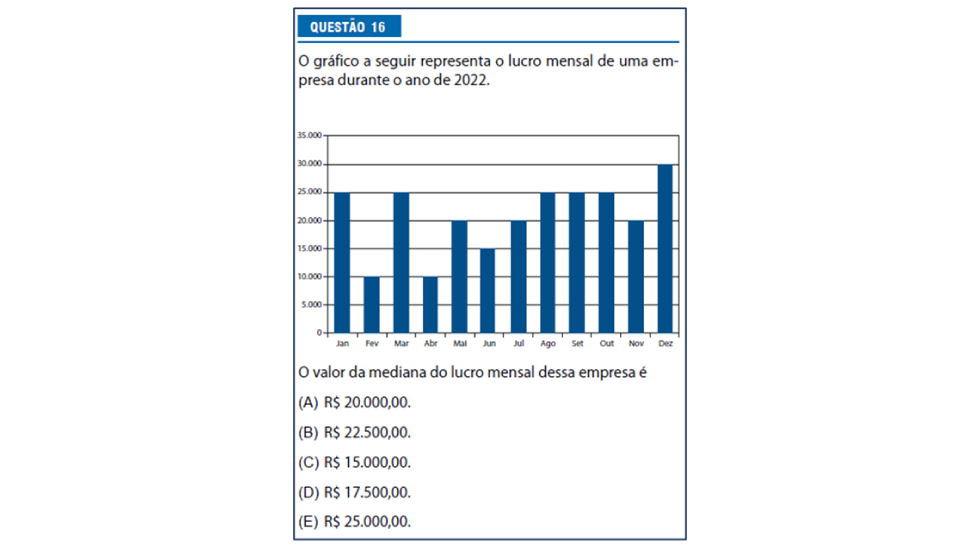
O problema apresenta um contexto de levantamento de dados financeiros, referentes ao lucro mensal de uma empresa, em que os dados estão indicados na forma de gráfico de colunas, de modo a favorecer a percepção das mudanças ocorridas ao longo do ano.
Nesse caso, a obtenção da resposta envolve dois passos centrais: a ordenação dos valores e o cálculo da mediana que, nesse caso, é a média do 6 e do 7 valores, já que o total de dados é um número par (12 valores). Com isso, chega-se a R$22.500,00 como valor central, alternativa (B), opção assinalada por cerca de 20% dos estudantes. Ou seja, apenas 1 em cada 5 alunos foi capaz de assinalar a alternativa correta.
A escolha das demais alternativas de resposta está atrelada a eventuais erros, destacados na sequência:
(A) R$20.0000,00 => o estudante provavelmente ordenou os dados e tomou como mediana o sexto valor da sequência, desconsiderando que, quando o conjunto possui uma quantidade par de dados, a mediana é obtida a partir da média aritmética de dois dados centrais;
(C) R$15.000,00 => valor referente ao sexto mês do gráfico, indicando erro similar ao da alternativa (A), agravado pela tomada da ordenação dos meses, em vez da ordenação dos valores;
(D) R$17.500,00 => alternativa mais próxima da correta, por assim dizer, uma vez que indica a média aritmética do 6 e 7 mês como resposta, sugerindo que o erro possivelmente está associado à preferência pela ordenação dos meses, e não pela ordenação dos valores.
(E) R$25.000,00 => valor da moda estatística, sugerindo possível equívoco entre as definições de moda e de mediana. Foi o distrator mais escolhido, sendo a opção de um terço dos que participaram do teste.
Na edição 2021 do SARESP, uma das questões propostas para os estudantes ao final do Ensino Médio, e apresentada na sequência, envolvia o conceito de mediana.
Figura 7 – SARESP 2021 – 3ª série EM

Tema central: mediana.
Percentual de acerto: 44,5%
Observação: os dados estão ordenados, diferentemente do que ocorreu na questão sobre os lucros mensais de uma empresa. Além disso, a quantidade de elementos é ímpar, ou seja, o valor da mediana é obtido de forma direta, sendo necessariamente um dos valores coletados, o valor central, mais especificamente.
Destaca-se a diferença no percentual de acerto, dado que o percentual observado no SARESP foi superior ao dobro do que foi observado no Provão Paulista. Contudo, há diferenças relevantes na formulação dos problemas, sugerindo que há uma quantidade de variáveis significativas a serem consideradas e investigadas pelo professorado da rede estadual. Para fins de exemplificação, será retomado o último exemplo do Provão Paulista citado anteriormente. Dentre as possíveis alterações, destacam-se:
i) os dados serem apresentados em uma tabela, em vez de um gráfico de colunas:
Os dados apresentados na sequência representam o lucro mensal de uma empresa no ano de 2022.
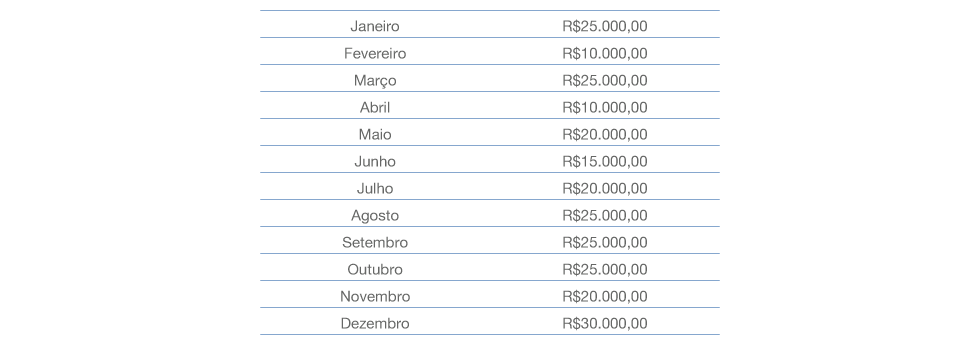
Com base nos dados apresentados, o valor da mediana dos lucros mensais dessa empresa é
ii) além de listados em uma tabela, os dados já estarem ordenados:
Ao longo do ano de 2022, uma empresa obteve diferentes lucros mensais. A tabela a seguir mostra os valores conquistados, ordenados do menor para o maior lucro obtido ao longo dos doze meses.
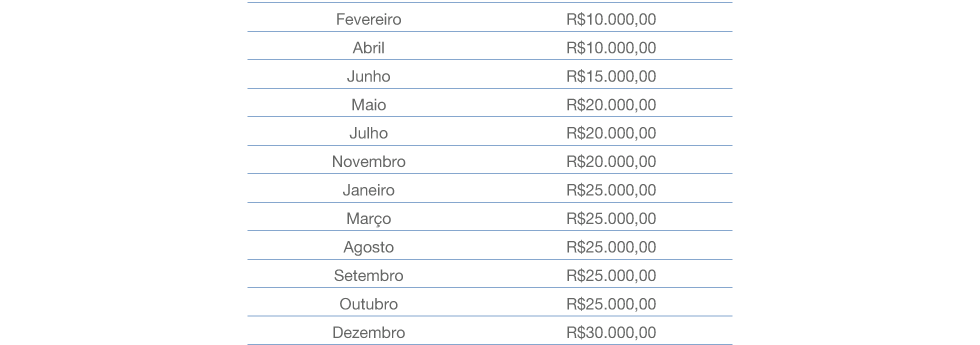
Com base nos dados apresentados, o valor da mediana dos lucros mensais dessa empresa é
iii) Uma tabela mais sofisticada, que comumente eleva o grau de complexidade, é a seguinte:
Os dados apresentados na tabela mostram o lucro mensal de uma empresa no ano de 2022 e a quantidade de meses para os quais aquele lucro foi obtido.

Com base nos dados apresentado, o valor da mediana dos lucros mensais dessa empresa é
iv) mudar o cenário da contextualização, de modo que seja analisado um número ímpar de valores. Por exemplo, um balanço do lucro anual dos últimos 15 anos.
O gráfico a seguir representa o lucro anual de uma empresa obtido nos últimos quinze anos.
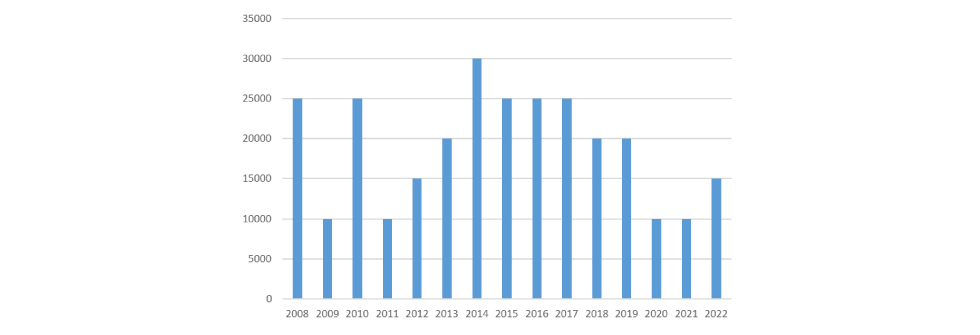
Com base nos dados apresentados, qual o valor da mediana do lucro anual dessa empresa para o período observado?
As observações feitas para (i) a (iii) também são possíveis variações a serem consideradas para o que foi posto em (iv), ampliando a quantidade de possibilidades a serem exploradas junto aos estudantes. Além das mudanças apresentadas na forma de apresentação dos dados, reitera-se a importância de serem feitas adequações de contextos abordados, de modo a fomentar discussões que promovam a percepção de equivalência de ideias entre cenários diversos.
Considerando-se que parte do alunado é capaz de resolver problemas como os apresentados aqui, também cabe indicar possibilidades para ideias mais complexas, como é o caso de problemas que envolvem médias aritméticas de parte/subgrupos dos elementos do conjunto; o que também pode ser associado à ideia de média aritmética ponderada. A seguir, tem-se a reprodução de uma questão apresentada no Provão Paulista e outra, no SARESP – edição 2021, essa última ancorada no ponto 400 da escala proficiência, compondo os descritores do nível Avançado.
Figura 8 – Provão Paulista – 3ª série EM

A solução desse problema pode ser obtida a partir de uma leitura inversa da definição de média, que é a ideia de que a soma das partes deve ser igual ao produto da média pelo número de partes. Segue:
Considere a nota dos vinte alunos identificadas por A1, A2, A3, ... A20. De acordo com as informações do enunciado, tem-se, de início, que:
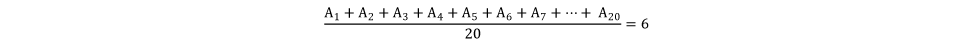
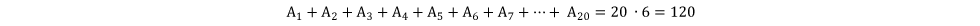
Pela mesma ideia, 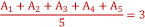 , ou seja, , ou seja,  . Assim sendo, é possível substituir o somatório dessas notas por 15 na expressão inicial. . Assim sendo, é possível substituir o somatório dessas notas por 15 na expressão inicial.
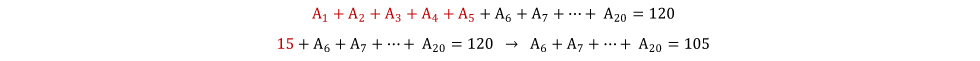
Logo, a média dessas 15 notas é dada por 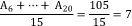 , alternativa (B). , alternativa (B).
Figura 9 – SARESP 2021 – 3ª série EM

Tema central: média aritmética ponderada.
Percentual de acerto: 24,2%
Observação: A solução dessa questão pode ser obtida de modo similar ao do exemplo anterior. Contudo, a ideia é mostrar outra possibilidade, usando a ideia de média ponderada. Aqui, cabe observar que a alternativa mais assinalada, opção (B), recai sobre a ideia de média aritmética simples, ignorando que a primeira e a segunda fase da competição apresentam número de jogos distintos. A média final seria equivalente à medida simples das médias de gols das fases se, e somente se, o número de jogos fosse o mesmo nas duas fases. Esse é um ponto central da discussão envolvendo o conceito de média que precisa ser cuidadosamente posto, discutido e trabalhado junto aos estudantes.
Uma maneira de solucionar o problema apresentado envolve perceber que a primeira fase é composta de 3 jogos e a segunda, de 4 jogos. Assim sendo, pode-se adotar o número de jogos como sendo o peso atribuído à média de gols das fases. Então, dado que, na primeira fase, a média foi 1 gol por partida e que, ao término da competição, a média foi 2 gols por partida, chamaremos de G a média de gols na segunda fase, de modo que as informações se relacionem da seguinte maneira:
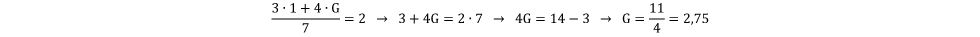
Com isso, espera-se chamar atenção para o fato de que a ideia de média ponderada não está unicamente atrelada a casos em que deliberadamente se anuncia que algum valor tem peso diferente dos demais. Há casos em que esse peso diferente entre as partes que compõem o problema precisa ser percebido, não estando claramente explicitado na problemática.
No caso da questão do Provão, apresentada na figura 8, pode-se considerar dois grupos, um composto de 5 alunos e outro composto por 15 alunos, em que se sabe a nota do primeiro grupo, mas não a do segundo, apesar de se ter a média dos 20 envolvidos. Assim, de modo análogo ao problema do saldo de gols da seleção francesa, tem-se que:
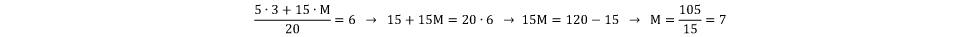
Esses cuidados com o tratamento de dados, para obtenção de medidas centrais, precisam estar presentes desde os Anos Finais do Ensino Fundamental. Contudo, é no Ensino Médio que isso precisa ser intensificado, inclusive com o uso de novas tecnologias para fazer o tratamento de conjuntos com mais quantidades de dados.
Essas nuances também podem ser trabalhadas nas aulas de outros componentes curriculares. Em Geografia, por exemplo, ao tratar dados do censo – taxa de urbanização, por exemplo – com os estudantes, o professorado poderá instigá-los a observar que a média nacional não corresponde à média aritmética simples dos estados, ao analisarem um conjunto de dados como o apresentado a seguir.
Figura 10 - Questão 20 - Processo Seletivo de Medicina 2017 - Universidade de Franca (Adaptado)
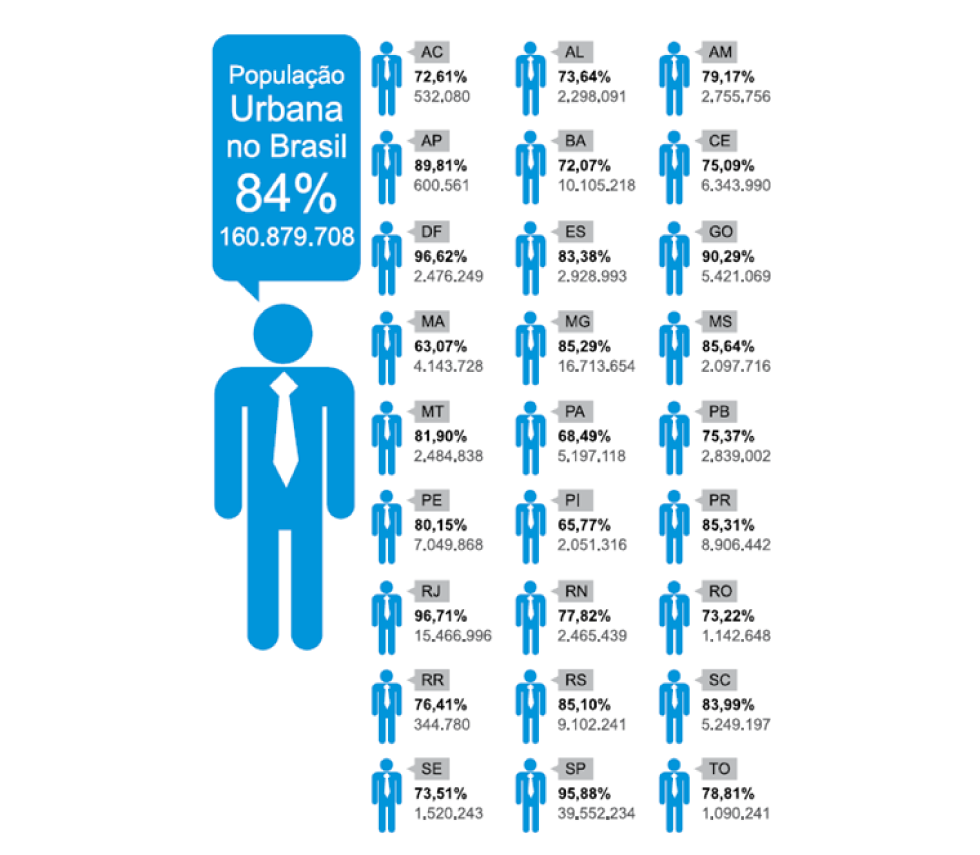
Uma vez que o motivo dessa divergência é exatamente o tamanho da população de cada estado, os alunos também podem debater o motivo de 18 unidades federativas estarem abaixo da média nacional e apenas 9 unidades federativas estarem acima, não havendo, portanto, uma distribuição mais próxima entre valores acima e abaixo da média nacional. Também é possível entender melhor o “peso” dos estados mais populosos nesse cálculo, modificando-os e analisando o impacto dessa alteração na média nacional.
Outra possibilidade, agora nas aulas de Química, é a obtenção da densidade de ligas metálicas a partir da densidade dos metais que as compõem, considerando a quantidade de metal usado na composição dessas ligas. Um contexto interessante que pode instigar a curiosidade dos estudantes são os testes de densidade para aferição de possível adulteração em barras de prata ou de ouro.
Por fim, há que se destacar a possibilidade de integração da temática Medidas Centrais com outros assuntos dentro da própria Matemática, quando o conhecimento a elas relacionado é apenas parte da solução. No exemplo a seguir, presente no teste aplicado para os estudantes da 2ª série EM, no Provão Paulista, o conceito de média aritmética simples foi atrelado ao de contagem.
Figura 11 – Provão Paulista – 2ª série EM

A solução depende de o aluno conhecer tanto os princípios da contagem como o cálculo da média aritmética. Nesse caso, uma ideia que leva à solução é a percepção de que, se o dígito central é a média dos vizinhos, então a soma dos números vizinhos é o dobro do dígito central; o que implica a soma dos dígitos vizinhos ser um número par, restringindo a possibilidade de opções para a obtenção da resposta. Obviamente, essa é uma ideia sofisticada para o Ensino Médio, mas que oportunamente pode ser apresentada para o alunado.
Encerra-se esse estudo reiterando a atenção aos pontos centrais aqui discutidos, juntamente à necessidade de a temática ser trabalhada levando em consideração os resultados aferidos pela avaliação externa, de modo a buscar reverter as dificuldades aqui listadas, o que não se limita somente aos responsáveis pelas aulas de Matemática.
| topo |

O presente estudo apresenta uma análise do desempenho dos estudantes no Provão Paulista em relação ao conteúdo de Conjunção, um componente curricular avaliado nas edições anteriores do SARESP e que foi solicitado no Provão Paulista de 2023, por essa razão, a temática selecionada permite comparar o desempenho obtido pelos estudantes nas referidas provas. Ademais, a escolha desse conteúdo tem relação direta não apenas com a importância que o estudo das conjunções tem para classificar um termo de acordo com a função desejada, em períodos ou orações, mas também para que os alunos compreendam as relações estabelecidas entre palavras e frases de um texto, o que necessariamente resulta em uma melhoria na produção textual estudantil.
Desse modo, a reflexão sobre o aprendizado das conjunções é produtiva para entender como se dá a aquisição de uma ferramenta linguística em prol de uma boa compreensão textual, conforme preconiza a Nova Base Comum Curricular (BNCC):
Cabe ressaltar, reiterando o movimento metodológico de documentos curriculares anteriores, que estudos de natureza teórica e metalinguística – sobre a língua, sobre a literatura, sobre a norma-padrão e outras variedades da língua – não devem nesse nível de ensino ser tomados como um fim em si mesmo, devendo estar envolvidos em práticas de reflexão que permitam aos estudantes ampliarem suas capacidades de uso da língua/linguagens (em leitura e em produção) em práticas situadas de linguagem. (BNCC – p. 71)
Partindo desse pressuposto, observa-se que diversas habilidades do Currículo Paulista preconizam o estudo das conjunções voltado para a compreensão desses articuladores textuais em um contexto mais amplo, que envolve leitura de textos variados, conforme observado nas habilidades a seguir.
(EF05LP07) Compreender, na leitura de textos, o sentido do uso de diferentes conjunções e a relação que estabelecem na articulação das partes do texto: adição, oposição, tempo, causa, condição, finalidade.
(EF05LP27B) Utilizar, na produção escrita de diferentes textos, articuladores (conjunções, advérbios e preposições) de relações de sentido (tempo, causa, oposição, conclusão, comparação), com nível adequado de informatividade, considerando a situação comunicativa, o tema/assunto, a estrutura composicional e o estilo do gênero.
(EF08LP13A) Analisar efeitos de sentido decorrentes do uso de recursos de coesão sequencial: conjunções e articuladores textuais.
Essas habilidades serviram de parâmetro para a construção de questões de edições anteriores do SARESP, demonstrando que a temática analisada no presente estudo é de conhecimento do estudante que realizou o Provão Paulista. Para exemplificar isso, apresenta-se a seguir uma questão aplicada aos estudantes do 9º ano do EF do SARESP 2022.
Figura 1 – SARESP 2022 – 9º ANO EF

A tarefa proposta exigiu a leitura e compreensão de um meme para solicitar ao aluno a identificação, nas alternativas de resposta, do efeito de sentido provocado pelo uso de um articulador textual, no caso, a conjunção “mas”. Embora a temática dessa questão seja amplamente conhecida pelos alunos tanto do 9º ano EF quanto da 3ª série EM, reconhece-se que os resultados obtidos na referida questão demonstram dificuldade para compreender o efeito de sentido desse termo, dado que apenas 18,8% dos alunos assinalaram o gabarito da questão, demonstrando conhecimento de que o termo apresentado expressa uma ideia de adversidade.
Finalizada a análise da questão aplicada no 9º ano EF SARESP 2022, serão apresentados exemplos de questões do Provão Paulista, em que a temática envolveu o uso de conjunções.
Figura 2 – Provão Paulista – 2ª série EM

O item apresentou ao aluno como contexto de leitura um trecho extraído de uma notícia. Na sequência, pede-se uma análise da conjunção “entretanto”, de modo a identificar em que sentido o uso desse termo contribui para o entendimento do trecho em análise. Nesse caso, a opção correta é a que apresenta o contraponto gerado pela conjunção “entretanto”, ao evidenciar que, apesar de representar um avanço social, a gramática antirracista ainda não é refletida na postura do Judiciário, alternativa (C), assinalada por 58,7% do alunado, percentual superior ao observado no exemplo citado anteriormente, presente em edição passada do SARESP. Embora apresente porcentagem inferior (12,3%), a segunda possibilidade de resposta mais assinalada, alternativa (B), revela dificuldade do aluno em compreender o uso da palavra “entretanto”, dado que essa alternativa apresenta o sentido oposto ao do termo. Menciona-se, ainda, que as demais alternativas (A), (D) e (E), que juntas totalizaram 29%, apontam para um uso totalmente equivocado do termo em análise.
Figura 3 – Provão Paulista – 2ª série EM

Ainda na 2ª série EM do Provão Paulista, há outra questão que contemplou o uso da conjunção adversativa “entretanto”. Nesse caso, exigiu-se que o alunado indicasse, entre as alternativas oferecidas, a que apresentasse termos ou locuções conjuntivas que poderiam substituir o termo em análise.
Como resultado, 30,1% dos alunos indicaram o gabarito alternativa – (D) –, 29,4% dos alunos optaram pela alternativa (C) e 20% deles assinalaram (E). A análise desses distratores revela que parte expressiva do aluno compreende muito bem o sentido expresso pelo termo “entretanto”, conseguindo inclusive substitui-lo por outro termo de mesmo sentido, uma que vez que (C) apresentou duas conjunções adversativas. Ocorre que, possivelmente, o alunado tenha tido dificuldade para compreender o sentido concessivo do termo “embora”, presente no referido distrator.
Neste momento, será realizada uma comparação entre as questões aplicadas à 3ª série do Ensino Médio do SARESP e do Provão Paulista, de modo a evidenciar semelhanças/divergências em relação ao desempenho dos alunos nessas provas.
Figura 4 – SARESP 2022 – 3ª série EM

A questão envolveu um contexto de leitura de uma tirinha para exigir que seja identificada a função da conjunção “ou”. Os resultados revelam que os alunos se saíram muito bem nessa questão, dado que 73,2% indicaram o gabarito como alternativa correta (A), reconhecendo que a referida conjunção tem a função de criar alternância no trecho analisado. Nota-se, ainda, que o distrator mais atrativo, com 10,6%, foi o da alternativa (C) que apresenta, de fato, uma possibilidade de uso da conjunção “ou”, porém, é preciso lembrar que não basta apenas indicar o uso correto na referida conjunção, deve-se analisar o contexto da tirinha de modo a observar que o uso do “ou” se refere necessariamente a uma relação de alternância entre os termos citados.
Figura 5 – Provão Paulista – 3ª série EM

A questão envolve a análise de palavras de modo a identificar, entre as alternativas de resposta, a que apresenta o sentido expresso no uso dos termos “mesmo” e “mesmo que”. O gabarito (D) foi assinalado por 10,4% dos alunos, indicando que provavelmente houve dificuldade com os conteúdos abordados nessa questão. Trata-se de uma dificuldade proposta pelo próprio item, dado que é exigido o sentido empregado por dois termos usados em situações distintas: sendo a primeira o uso do termo “mesmo” utilizado como um advérbio de inclusão, um acréscimo de um elemento; já a segunda, o uso da conjunção concessiva “mesmo que”.
Ressalta-se que a formulação dessa questão, em comparação com a da Figura 4 aplicada no Saresp, evidencia um trabalho a mais para o aluno, já que a análise da conjunção é parte da solução, mas é necessário observar ainda o sentido usado pelo advérbio presente na passagem do texto em análise.
Figura 6 – Provão Paulista – 3ª série EM

Nessa questão, o aluno precisou demonstrar o conhecimento sobre o uso da locução “apesar de” no trecho destacado, algo que foi bem assimilado por 39,7% dos alunos que optaram pelo gabarito (B). Tais alunos identificaram que a referida locução expressa uma ideia contrária em relação ao que se esperava sobre a crise ambiental canadense, havendo uma quebra de expectativa concretizada pelo uso da expressão “apesar de”.
Em relação ao SARESP, nota-se que o percentual de acerto dessa questão do Provão Paulista foi bem menor, mas é importante destacar que a diferença entre a formulação das questões se apresenta como um notório aspecto a ser observado. Desse modo, mesmo havendo semelhança no conteúdo avaliado – o uso de conjunção – há aspectos que são específicos de cada projeto, exigindo uma seleção de textos apropriados para dar ao aluno a condição mínima de uma análise textual.
Para finalizar esse breve estudo, destaca-se mais uma vez que a comparação entre as provas do SARESP e Provão Paulista traz discussões produtivas para a sala de aula, uma vez que permite observar como o alunado compreendeu determinado conteúdo ao longo de sua vida escolar até chegar a um processo seletivo que pode garantir uma vaga em uma universidade pública. Assim, os desafios apresentados neste estudo configuram como pontos específicos que podem ser trabalhados em sala de aula para haver, de fato, uma melhoria nos enfrentamentos aqui apontados.
| topo |
De modo simplificado, segundo BERGO et al (1998), o scout é um método numérico que processa dados sobre determinada equipe durante as partidas, como número de passes, faltas, desarmes, ou seja, recolhe informações de várias situações envolvidas em um jogo.
(In: BERGO, F.P.G.; ANIDO, R.; BARROS, R.M.L.; CUNHA, S.A.; FREIRE, J.B. Software para análise topológica de ações no futebol. In: SIMPÓSIO INTERNACIONAL DE CIÊNCIAS DO ESPORTE, 21., 1998, São Caetano do Sul. Anais. São Caetano do Sul: CELAFISCS, 1998. p.90.).
voltar
|
 |
|
 |
| |
|
|