|
 |
Na edição de 2023 do SARESP, a participação dos estudantes da rede estadual na aplicação das provas do 2º e 5º ano do EF foi de 89,6% e 93,8%, respectivamente. Esses percentuais de participação dos alunos são superiores aos observados na edição anterior e permitem a obtenção de dados robustos da realidade escolar, trazendo representatividade e maior segurança ao processo; o que é fundamental tanto para a aferição da proficiência da rede escolar como para indicar os fatores que influenciam no desempenho escolar.
A seguir, tem-se um histórico da média de proficiência aferida para esses dois anos escolares nas últimas quatro edições, de 2019 a 2023.

Enquanto o resultado de Matemática para o 2º ano apresentou oscilação, sugerindo um movimento de avanço ainda não consolidado, os dados obtidos no 5º ano apontam para uma melhora no período 2021-2023, mesmo que discreta. Entretanto, os resultados aferidos nesta edição para o 5º ano EF são inferiores àqueles obtidos em 2019, último ano antes da pandemia de Covid-19. Vale destacar que somente a partir de 2021 os resultados do 2º ano EF passaram a ser obtidos na mesma escala dos demais anos avaliados pelo SARESP. Logo, não há como estabelecer comparativo com o ano de 2019.
Além da medida de proficiência obtida, os resultados permitem atrelar o desempenho dos estudantes na prova aos níveis de proficiência da escala SARESP. Os gráficos apresentados a seguir exibem os resultados obtidos na série histórica das provas dos anos iniciais do Ensino Fundamental.
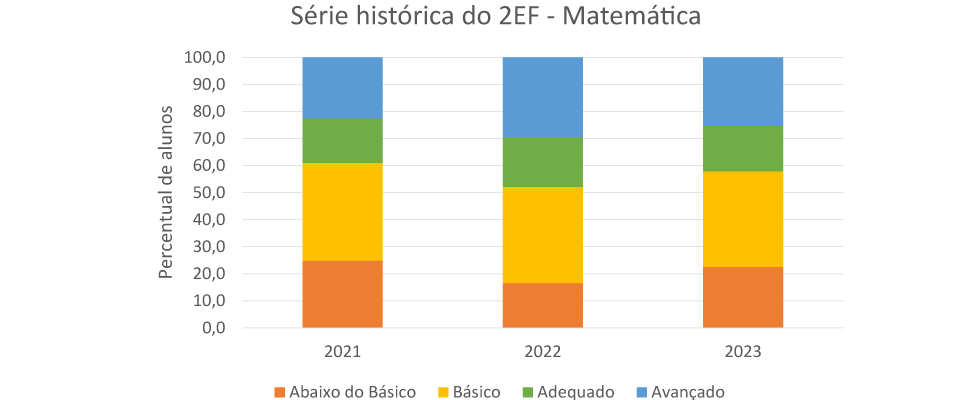
Os resultados do 2º ano EF apontam para uma oscilação na distribuição dos estudantes nos níveis de proficiência ao longo do triênio avaliado. Isso sugere que a melhora observada em 2022 não se consolidou na rede, visto que os resultados de 2023 são mais próximos aos obtidos em 2021. Ainda assim, quase 80% dos alunos que concluíram esse ano escolar desenvolveram minimamente as habilidades esperadas. Além disso, praticamente 25% do alunado é capaz de resolver tarefas mais complexas do que as previstas para a etapa escolar. Apesar de relevante, esse resultado é discreto se comparado ao de Língua Portuguesa, em que metade dos estudantes demonstra proficiência associada ao nível Avançado.
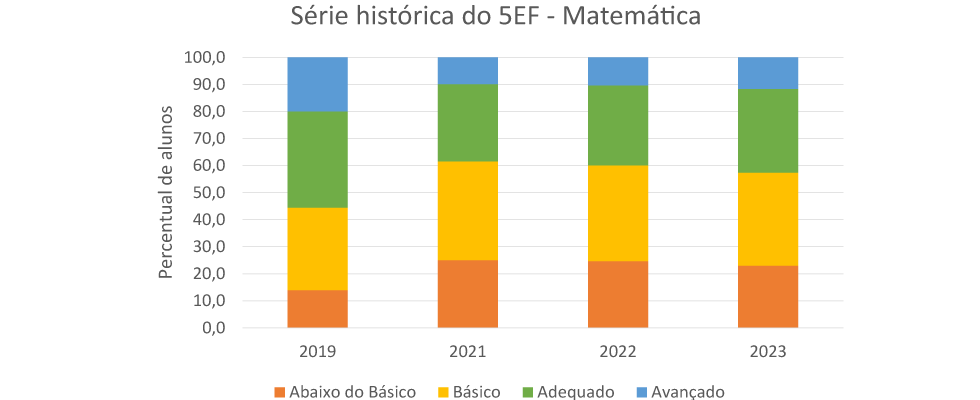
Já em relação aos resultados do 5º ano EF, observa-se uma redução no percentual de estudantes no nível Abaixo do Básico no triênio 2021-2023. Entretanto, no comparativo com 2019, constata-se que ainda há bastante trabalho pela frente para alcançar tais resultados, em especial no que se refere a esse nível, considerando tratar-se de estudantes que demonstram domínio insuficiente dos conteúdos, das competências e das habilidades desejáveis para o ano escolar em que se encontram. Sendo assim, quando se fala em fechamento de ciclo e nas mudanças decorrentes do ingresso no 6º ano, é fundamental que esses alunos sejam assistidos de perto, em intenso processo de retomada e recuperação. Em contrapartida, cabe apontar que os dados da edição 2023 revelam que 3 em cada 4 estudantes que concluíram o 5º ano EF na rede estadual garantidamente desenvolveram os conhecimentos mínimos necessários para a continuidade da trajetória escolar.
Cada edição do SARESP é organizada com base em um conjunto de 56 itens (questões) para o 2º ano EF e 104 itens (questões) para o 5º ano EF. A partir desse montante, são elaborados diferentes cadernos de provas, que são distribuídos entre os alunos de determinada escola. Parte desse montante é composta de itens de edições anteriores para garantir a comparabilidade dos resultados. A outra parte é composta de itens inéditos com novas tarefas, visando, assim, ampliar o leque de informações sobre os conhecimentos escolares que os estudantes se mostraram capazes de mobilizar para resolver situações-problema. Essa capacidade de mobilizar conhecimento para resolver problemas é o que se entende por proficiência; havendo casos mais simples de serem resolvidos, assim como outros mais complexos. Com base no grau de complexidade desses problemas e na organização deles na prova, é criada a chamada escala de proficiência. Nesse sentido, a edição de 2023 contribuiu com a inclusão dos descritores dos itens inéditos na escala de proficiência, apresentados a seguir.

Clique nos níveis de proficiência para ver a descrição das novas tarefas inseridas na escala de proficiência, obtidas no SARESP 2023 e o percentual de alunos que respondeu corretamente cada uma dessas tarefas.
2º ano EF
Abaixo do Básico
Básico
Adequado
Avançado
Abaixo do Básico
X Fechar
• Não há novos descritores na prova de 2023 para esse nível
Básico
X Fechar
• Comparam comprimentos entre quatro setas, com o apoio de malha quadriculada, para identificar a seta mais comprida.
• Comparam os números naturais 12, 14, 15 e 17, que representam idades, pela compreensão de características do sistema de numeração decimal e identificam a idade da pessoa mais velha.
• Constroem fatos básicos da multiplicação e os utilizam em procedimentos de cálculo para resolver problema, com o apoio de imagem, no qual é necessário determinar o total de patas em um conjunto de 5 vacas.
• Identificam na malha quadriculada o estabelecimento de um bairro que está localizado na coordenada 5B (posto de combustível).
• Identificam que a forma geométrica plana “quadrado” compõe as faces do cubo.
• Leem o número 128 presente no bilhete que indica a numeração de um assento em um espetáculo e identificam o seu registro por extenso, estabelecendo relação entre o registro numérico e em língua materna.
• Leem o número por extenso “quarenta e cinco” e identificam o seu registro com algarismos nas cartelas de bingo apresentadas, estabelecendo relação entre o registro numérico e em língua materna.
• Leem o número por extenso “trinta e quatro” e identificam o seu registro com algarismos, estabelecendo relação entre o registro numérico e em língua materna.
• Organizam figuras geométricas planas coloridas em grupos por meio do atributo forma.
• Reconhecem e comparam figuras geométricas espaciais, relacionando-as com objetos presentes na cozinha e determinam o que se assemelha a um cone (peneira cônica), com referência da imagem dessa figura espacial.
• Reconhecem e nomeiam o objeto, dentre os apresentados, que se assemelha a figura geométrica pirâmide.
• Reconhecem e relacionam valores de moedas e cédulas do sistema monetário brasileiro para identificar, dentre quatro valores apresentados, qual representa o valor exato de R$ 7,00.
• Resolvem situação-problema de adição, com significado de juntar, na qual se deve somar 9 meninos e 7 meninas de uma turma para determinar o total de alunos.
Adequado
X Fechar
• Comparam informações apresentadas por meio de um gráfico de colunas simples que indica as brincadeiras preferidas de um conjunto de crianças e identificam a segunda brincadeira mais votada.
• Comparam quatro números naturais da ordem da dezena (45, 12, 37 e 25) e os ordenam de maneira crescente pela compreensão de características do sistema de numeração decimal.
• Compõem o número 329 por meio da adição “200 + 100 + 20 + 9”.
• Constroem fatos básicos da adição e os utilizam no cálculo da adição das parcelas 155 e 24.
• Constroem fatos básicos da divisão e os utilizam em procedimentos de cálculo para resolver um problema, com apoio de imagem, no qual é necessário dividir igualmente 10 camisas em grupos de 2.
• Descrevem o elemento ausente em uma sequência recursiva de números naturais, que está aumentando de 2 em 2, cujo número está entre 26 e 30.
• Descrevem o elemento ausente em uma sequência recursiva de números naturais que está aumentando de dois em dois, cujo número está entre o 40 e o 44.
• Leem o número por extenso “trezentos e quarenta e dois” e identificam o seu registro com algarismos, estabelecendo relação entre o registro numérico e em língua materna.
• Produzem a escrita de uma data que indica o dia da semana (quinta-feira) em que se iniciou um determinado mês (setembro de 2011), consultando o calendário.
• Resolvem situação-problema de adição de parcelas iguais, utilizando suporte de imagem, para determinar a quantidade de miçangas necessárias para fazer 4 pulseiras com 12 miçangas cada uma.
Avançado
X Fechar
• Classificam o resultado do sorteio de uma ficha amarela no universo de 17 fichas coloridas como “pouco provável”.
• Estabelecem a equivalência de valores entre duas moedas no valor de R$ 0,50 e quatro moedas no valor de R$ 0,25 cada a uma cédula de R$ 2,00.
• Leem e registram medida de intervalo de tempo, utilizando relógio digital, para determinar o horário de início de uma aula de natação (15h10), dado o horário de término (16h00) e sua duração (50 minutos).
• Medem a duração de um intervalo de tempo para percorrer o trajeto entre a casa e a escola de uma menina, por meio de relógio digital, que indica o horário de saída de casa (12h05) e o horário de chegada na escola (12h25).
• Resolvem situação-problema de subtração, envolvendo números da ordem da dezena, com o significado de retirar, ao descobrir a quantidade de lápis de uma pessoa, dada a quantidade total (30) e a da outra pessoa (17).
• Resolvem uma situação-problema de compra de um estojo de R$ 20,00 com uma nota de R$ 50,00 e indicam a alternativa cujo troco está correto, composto por uma nota de R$ 20,00 e duas notas de R$ 5,00.
5º ano EF
Abaixo do Básico
Básico
Adequado
Avançado
Abaixo do Básico
X Fechar
• Não há novos descritores na prova de 2023 para esse nível
Básico
X Fechar
• Identificam a representação da fração 1/6, associando-a à ideia de uma parte de um círculo dividido igualmente em 6 partes.
• Identificam características do sistema de numeração decimal para decompor o número 1375 em suas ordens (1 unidade de milhar + 3 centenas + 7 dezenas + 5 unidades).
• Identificam na malha quadriculada o estabelecimento colocado por Gabriel, na sua cidade fictícia em um jogo, que está localizado na coordenada 4D (banco), a fim de desenvolver noções de coordenadas cartesianas.
• Leem e ordenam um número positivo na forma decimal (12,3), identificando sua posição na reta numérica.
• Leem e registram medidas de tempo em horas e minutos para determinar o horário final de cozimento de um ovo, dado o horário de início do cozimento (10h50) e o tempo de cozimento (12 minutos).
• Leem o número 7945 e identificam, a partir das regularidades do sistema de numeração decimal, a ordem a que pertence o algarismo 7 (unidade de milhar).
• Resolvem situação-problema de adição com números naturais para determinar o total de jogos de uma coleção, dada a quantidade inicial (24268) e a quantidade que será comprada (1700), utilizando estratégias diversas.
• Resolvem situação-problema de multiplicação envolvendo números racionais, para determinar a distância percorrida por Julia de sua casa até a escola, sabendo-se que é o dobro da distância percorrida por João.
• Resolvem situação-problema de subtração com números naturais para determinar o valor do feijão, dado o total da compra (R$ 39,00) e os valores dos demais produtos (R$ 12,00, R$ 9,00 e R$ 6,00).
• Resolvem situação-problema que envolva variação de proporcionalidade direta entre duas grandezas (1 forno assa 40 bolos por dia), associando a quantidade de bolos produzidos com o uso de 3 fornos iguais.
Adequado
X Fechar
• Analisam e interpretam dados estatísticos apresentados em gráfico de colunas sobre arrecadação de materiais recicláveis, para determinar a diferença em quilogramas entre o material de maior e de menor arrecadação.
• Associam a representação 10% à décima parte, para calcular a massa de areia de uma preparação para fazer tijolos (10% de 10 Kg = 1 Kg), utilizando estratégias pessoais.
• Associam a representação 25% à quarta parte, para calcular porcentagem e determinam que 25% do total de 60 litros de leite, que se pretende arrecadar, corresponde a 15 litros.
• Associam a representação 25% à quarta parte para calcular o valor da entrada de um carro de R$ 40 mil (25% de 40 mil = 10 mil), utilizando estratégias pessoais.
• Associam a representação 50% à metade para calcular o valor de um jogo de R$ 60,00 após o desconto dessa porcentagem (R$30,00), utilizando estratégias pessoais.
• Calculam o perímetro de uma sala quadrada, sendo o comprimento de cada lado de 8 metros (8 x 4 = 32 metros).
• Determinam o número desconhecido que torna verdadeira a igualdade “8 x 3 = 6 + __”, envolvendo operações fundamentais com números naturais.
• Leem e ordenam em ordem crescente os números naturais até a ordem da centena de milhar (1270, 36840, 15770, 187591, 2016), a partir da compreensão das características do sistema de numeração decimal.
• Leem os números presentes nas alternativas e identificam, a partir das regularidades do sistema de numeração decimal, em qual deles o algarismo 5 ocupa a ordem em que seu valor posicional corresponde a 50.
• Leem os números presentes nas alternativas e identificam, a partir das regularidades do sistema de numeração decimal, em qual deles o algarismo 8 ocupa a ordem em que seu valor posicional corresponde a 800.
• Resolvem situações-problema cujos dados estão apresentados em um gráfico de colunas, para determinar qual o tipo de desenho animado teve entre 15 e 20 votos (robôs).
• Resolvem situação-problema de adição e subtração com números naturais, utilizando estratégias diversas, para determinar o valor total acumulado de uma pessoa que inicialmente tinha R$ 100,00, gastou R$ 40,00 e ganhou R$ 60,00.
• Resolvem situação-problema de adição com números racionais, para determinar a distância total percorrida em dois dias em uma viagem de bicicleta, dada a quilometragem do 1º dia (74,6 Km) e do 2º dia (62,5 Km).
• Resolvem situação-problema de divisão para determinar a quantidade de animais silvestres resgatados e divididos igualmente por centros de triagem (3928 ÷ 8 = 491), utilizando estratégias diversas.
• Resolvem situação-problema de multiplicação para determinar a quantidade de pedras necessárias para produzir 24 joias com 8 pedras cada (24 x 8 = 192), utilizando estratégias diversas.
• Resolvem situação-problema de multiplicação envolvendo números racionais, para determinar o valor total de rendimento de um investimento, dado a quantidade de dias (12) e o valor que rende a cada dia (R$3,50).
• Resolvem situação-problema de subtração com números naturais para calcular a diferença entre revistas arrecadas pelo grupo de alunos da manhã e da tarde (346 – 154 = 192), utilizando estratégias diversas.
• Resolvem situação-problema de subtração com números naturais para determinar o ano de nascimento de uma tartaruga, dado o ano em questão (2023) e a sua idade (191 anos), utilizando estratégias diversas.
• Resolvem situação-problema de subtração com números racionais, para determinar a diferença entre o tempo de um robô e de um velocista para percorrer 100 m (24,73 – 9,58 = 15,15), utilizando estratégias diversas.
• Resolvem situação-problema simples de contagem envolvendo o princípio multiplicativo, para determinar o número de agrupamentos possíveis ao se combinar 4 tipos de suco e 3 tipos de salgados.
• Resolvem situação-problema simples de contagem envolvendo o princípio multiplicativo, para determinar o número de agrupamentos possíveis ao se combinar 5 lápis com 4 blocos de anotação (5 x 4 = 20).
• Resolvem situação-problema simples de contagem envolvendo o princípio multiplicativo, para determinar o número de combinações possíveis ao se combinar 4 tipos de vegetais com 3 tipos de carne (4 x 3 = 12).
• Resolvem situação-problema que envolva variação de proporcionalidade direta entre duas grandezas (3 baldes para tanque de 14 L), associando a quantidade de baldes necessários para encher um tanque de 28 L.
• Resolvem situação-problema que envolve cálculo de troco, dado que foram gastos R$ 18,15 na compra de laços e essa compra foi paga com uma nota de R$ 20,00 (R$ 20,00 – R$ 18,15 = R$ 1,85).
Avançado
X Fechar
• Calculam a área de um painel retangular para a compra de tecido, dadas as medidas de comprimento de suas laterais (3 x 2 = 6 m²).
Calculam o perímetro de um convite, cujo formato é de um trapézio, dadas as medidas de todos os lados da figura (6 + 6 + 2 + 2 + 3 + 3 = 22 centímetros).
• Identificam diferentes escritas nas representações fracionária com o apoio em representações gráficas, determinando que as frações 4/8, 2/4 e ½ são equivalentes.
• Identificam diferentes escritas nas representações fracionária, identificando que a fração 2/8 em relação a um determinado percurso corresponde a fração equivalente 4/16 desse mesmo percurso.
• Leem e interpretam dados apresentados em tabela simples sobre itens encontrados em um sítio arqueológico em Roraima, para determinar a quantidade de itens que seriam expostos (3 tipos de 4 listados).
• Medem a área de um retângulo desenhado na malha quadriculada, pela contagem dos quadrados das laterais (7 x 11), dado que cada quadrado da malha corresponde a 1m².
• Produzem a escrita na representação decimal (0,5) a partir da representação gráfica de um círculo dividido igualmente em 8 partes, com 4 dessas pintadas (4/8=1/2=0,5).
• Reconhecem a proporcionalidade entre os lados correspondentes de uma imagem retangular em situação de redução pela metade, com apoio de malha quadriculada.
• Resolvem situação-problema que envolva proporcionalidade direta entre duas grandezas, para associar a quantidade de pessoas vacinadas a de frascos de vacina necessários (3 frascos para 18 pessoas, então, 24 frascos para 144 pessoas).
• Resolvem situação-problema de subtração, com números racionais, para determinar quantas gramas uma barra de chocolate diminuiu, dada a gramatura anterior (400 g) e a gramatura atual (250,6 g).
• Resolvem situação-problema envolvendo medida de área, com o apoio da malha quadriculada, para determinar a área de uma figura que ocupa 14 quadrados e cada um equivale a 100 cm² (14 x 100 = 1400 cm²).
• Resolvem situação-problema envolvendo a partilha de 500 inscrições de bolsas de estudos em duas partes desiguais, sendo que uma parte corresponde ao triplo da outra (125 e 375).
De modo simplificado, pode-se dizer que, quanto maior a proficiência média de uma turma em relação à posição do item na escala, maior é a probabilidade de a tarefa ser respondida corretamente. Lembrando que a proficiência média resulta dos desempenhos dos alunos dessa turma na prova e que esses desempenhos são díspares pois refletem estágios desiguais de aprendizagem da turma, já que uns dominam mais algumas habilidades do que outros. Por isso, é importante ter clareza de que o fato de a proficiência média de uma turma ser igual a 220, por exemplo, não permite afirmar que todos os alunos daquela turma demonstram proficiência 220.
Assim sendo, para essa turma, é esperado que esses alunos tenham maiores chances de acertar itens como aqueles descritos nos pontos 150, 175 e 200. Por outro lado, para os itens descritos em pontos mais altos da escala, a chance de acerto existe, mas é reduzida; de modo que é esperado que uma parcela pequena desses alunos seja capaz de acertar uma tarefa que está ancorada nos pontos 300 ou superior. Para saber o percentual de alunos capaz de lidar com essas tarefas ancoradas nos pontos mais altos da escala, é preciso analisar o boletim da escola e identificar o contingente de estudantes que estão distribuídos nos níveis mais altos da escala.
Uma estratégia que o professorado pode adotar é encontrar na Escala de Proficiência outros descritores relacionados às tarefas e habilidades. Com isso, é possível elaborar situações-problema com diferentes níveis de complexidade, iniciando das menos complexas, situações-problema mais simples, associadas à mesma habilidade e objeto do conhecimento, e que possam ser resolvidas por estudantes com menor proficiência, ou seja, iniciar por itens posicionados em pontos anteriores da Escala.
Nesse sentido, é de grande importância que os professores e gestores se valham de consultas à Descrição da Escala de Proficiência, que traz não apenas os itens âncoras, aplicados no SARESP 2023, como também a descrição de todos os outros itens aplicados em edições anteriores. Além disso, ela apresenta a posição de determinado item na Escala, isto é, a proficiência requerida dos estudantes de determinado ano/série, para que o item seja respondido com alta probabilidade de acerto.

Para saber mais sobre a escala de proficiência, encontrar sugestões de como utilizá-la e os descritores obtidos ao longo das edições do SARESP, clique aqui.
Na sequência, são apresentados os dados estatísticos que indicam como as provas aplicadas se comportaram em relação ao índice de dificuldade dos itens e respectivo índice de discriminação.
Dificuldade X Discriminação dos itens da prova do 2º ano EF
DIFICULDADE
Indica o percentual de alunos que respondeu corretamente o item. Quanto maior esse índice, mais fácil foi a tarefa proposta para ele resolver.
Esse índice é dividido em 5 categorias:
Muito Fácil: percentual de acerto superior a 85%
Fácil: percentual de acerto entre 65% e 85%
Médio: percentual de acerto entre 35% e 65%
Difícil: percentual de acerto entre 15% e 35%
Muito Difícil: percentual de acerto inferior a 15%
DISCRIMINAÇÃO
Índice que analisa o percentual de acerto em dois grupos, chamados de menor e de maior desempenho, que correspondem a um recorte dos alunos da turma que realizaram a prova. O grupo de menor desempenho é constituído por aproximadamente 27% dos estudantes que obtiveram os menores escores (número de acertos) em toda a prova de matemática. Analogamente, o grupo de maior desempenho também possui contingente parecido do aluno, mas que obtiveram os maiores escores na prova. O índice de discriminação é calculado a partir da diferença do percentual de acerto desses dois grupos no item, sendo que seu propósito é comparar o desempenho desses dois grupos opostos na realização de uma determinada tarefa proposta na prova, verificando assim se o item apresentado tem a propriedade de diferenciar o desempenho daqueles que obtiveram os melhores resultados no teste daqueles que conquistaram os resultados mais tímidos. Em geral, índices de discriminação mais baixos normalmente são observados em itens extremos, ou seja, considerados muito fáceis, em que uma imensa maioria acerta, ou de itens muitos difíceis, que estão relacionados a ideias mais complexas e que se mostraram pouco consolidadas, mesmo para estudantes com bons desempenhos gerais na área de conhecimento. Em contrapartida, itens com bons índices de discriminação decorrem de tarefas cujo conhecimento necessário para sua resolução está bem consolidado no grupo de maior desempenho, mas não está para o grupo de menor desempenho.
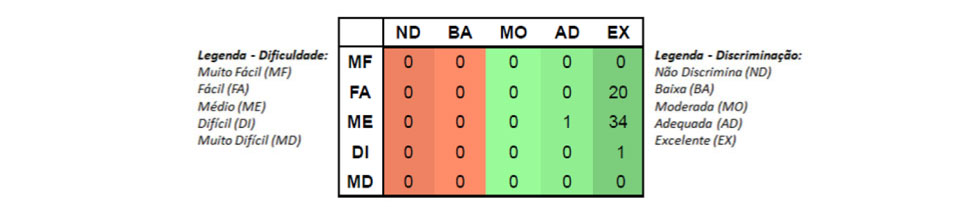
Podemos notar que a prova do 2º ano EF não apresentou itens com índices ruins de discriminação, uma vez que as colunas em tons alaranjados estão zeradas. Além disso, é possível observar a quantidade de itens difíceis na prova, apenas 2. Com isso, a prova acabou sendo composta quase que inteiramente de itens medianos ou fáceis; o que sugere haver condições de aumentar a complexidade dela em edições futuras.
Dificuldade X Discriminação dos itens da prova do 5º ano EF
DIFICULDADE
Indica o percentual de alunos que respondeu corretamente o item. Quanto maior esse índice, mais fácil foi a tarefa proposta para ele resolver.
Esse índice é dividido em 5 categorias:
Muito Fácil: percentual de acerto superior a 85%
Fácil: percentual de acerto entre 65% e 85%
Médio: percentual de acerto entre 35% e 65%
Difícil: percentual de acerto entre 15% e 35%
Muito Difícil: percentual de acerto inferior a 15%
DISCRIMINAÇÃO
Índice que analisa o percentual de acerto em dois grupos, chamados de menor e de maior desempenho, que correspondem a um recorte dos alunos da turma que realizaram a prova. O grupo de menor desempenho é constituído por aproximadamente 27% dos estudantes que obtiveram os menores escores (número de acertos) em toda a prova de matemática. Analogamente, o grupo de maior desempenho também possui contingente parecido do aluno, mas que obtiveram os maiores escores na prova. O índice de discriminação é calculado a partir da diferença do percentual de acerto desses dois grupos no item, sendo que seu propósito é comparar o desempenho desses dois grupos opostos na realização de uma determinada tarefa proposta na prova, verificando assim se o item apresentado tem a propriedade de diferenciar o desempenho daqueles que obtiveram os melhores resultados no teste daqueles que conquistaram os resultados mais tímidos. Em geral, índices de discriminação mais baixos normalmente são observados em itens extremos, ou seja, considerados muito fáceis, em que uma imensa maioria acerta, ou de itens muitos difíceis, que estão relacionados a ideias mais complexas e que se mostraram pouco consolidadas, mesmo para estudantes com bons desempenhos gerais na área de conhecimento. Em contrapartida, itens com bons índices de discriminação decorrem de tarefas cujo conhecimento necessário para sua resolução está bem consolidado no grupo de maior desempenho, mas não está para o grupo de menor desempenho.
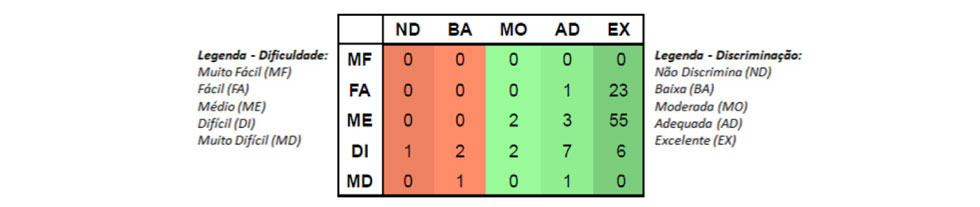
A prova do 5º ano EF praticamente não apresentou questões com índices ruins de discriminação, visto que há somente quatro itens destacados nas colunas em tons alaranjados. Esse comportamento de itens com discriminação ruim revela que, no caso de itens difíceis ou muito difíceis, além de o desempenho do público em geral em relação a eles ter sido ruim, os alunos com melhor desempenho geral na prova, isto é, aqueles que acertaram maior número de itens tiveram desempenho tímido na questão, muito próximo de todo o público avaliado.
Além disso, tem-se que a prova foi composta por uma maioria (pouco mais de 57%) de questões consideradas medianas. As demais se dividiram quase que igualmente entre questões fáceis e difíceis, indicando uma prova equilibrada no quesito grau de dificuldade.
Por fim, serão apresentados dois estudos, com base em exemplos de itens de múltipla escolha presentes na prova de Matemática do SARESP 2023, do 2º ano EF e do 5º ano EF. Os itens enquadram-se em duas habilidades, uma da unidade temática Números e a outra de Grandeza e Medidas.
O objetivo é apresentar aos docentes uma breve análise dos acertos e erros observados, além de destacar a importância das alternativas elaboradas para identificar possíveis equívocos comuns na resolução dos problemas propostos.
Traçou-se um paralelo entre os itens do 2º ano e 5º ano, pois é esperado que as habilidades se consolidem e sejam ampliadas no decorrer da escolaridade do aluno. É importante destacar que os alunos do 5º ano, devido à pandemia de Covid-19, realizaram o 2º e 3º anos de maneira não presencial, assim como os alunos do 2º ano tiveram tal prejuízo durante a Educação Infantil.
Mais do que simplesmente identificar erros e acertos, é essencial compreendê-los e considerá-los como parte do processo de aprendizagem. Compreender as dificuldades apresentadas pelos alunos pode auxiliar em alguma medida o professor a nortear o seu planejamento. Portanto, é crucial que esses itens sejam analisados juntamente com as considerações sobre a escala de proficiência e a discussão dos resultados de Matemática, sempre tendo como referência os resultados específicos da sua escola, conforme descrito no boletim SARESP.
Conforme posto, os exemplos foram escolhidos de acordo com duas habilidades. Clique naquela em que deseja fazer o download do documento produzido.
 |
|
 |
|
 |
|

|
| |
|
|