|
|
 |
A edição 2019 do SARESP aferiu a proficiência dos estudantes do 9º Ano do Ensino Fundamental, sendo que a média obtida foi igual a 259,9. Esse valor indica um nível de proficiência classificado como Básico para a turma em questão. Destaca-se, nesse ano escolar, a retomada no crescimento da proficiência média e a discreta melhora no percentual de alunos que ocupam os níveis Adequado e Avançado, totalizando 20,2% do alunado.
A seguir, são apresentados exemplos comentados a fim de ilustrar atividades características que os alunos foram capazes de realizar ou que demonstraram dificuldades. Além do enunciado e da solução dos itens, há a indicação de alternativas de trabalho, além de uma representação gráfica da frequência de escolha de cada alternativa nos três Grupos de Desempenho e a Curva Característica do Item que associa a proficiência do respondente e a probabilidade de acertar a questão.
Exemplo 1
Nível Básico
Compõe a descrição do ponto 275 da Escala de Matemática – SARESP

O item está atrelado a habilidade H21 – Reconhecer a semelhança entre figuras planas, a partir da congruência das medidas angulares e da proporcionalidade entre as medidas lineares correspondentes – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o assunto é tratada no 3º bimestre do 9º Ano do Ensino Fundamental. A tarefa proposta no item envolve reconhecer a semelhança entre duas figuras para determinação da medida do lado faltante na figura.
A solução pode ser obtida por meio da comparação entre os lados correspondentes dos triângulos RST e UVX.

A partir da comparação é possível perceber que as medidas informadas dos lados do triângulo UVX são a metade das medidas presentes no triângulo RST. Portanto, o lado UV tem que medir metade do lado RS, ou seja, metade de 10 cm. Sendo assim, obtém-se que o lado UV mede 5 cm.
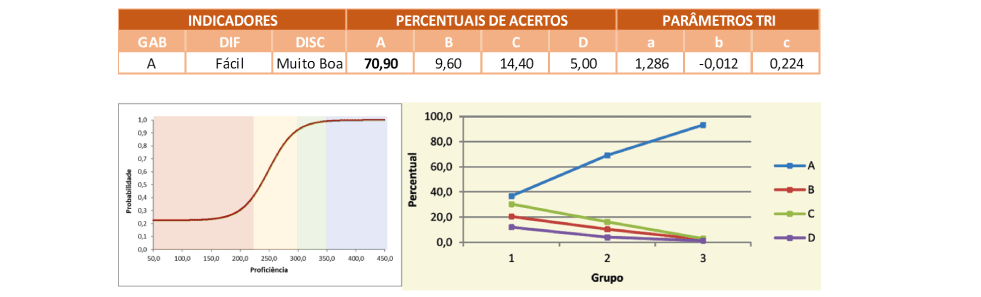
O item foi respondido corretamente por pouco mais de 70% dos estudantes, sendo que a alternativa correta foi a mais assinalada em todos os Grupos de Desempenho, porém, no Grupo de Menor Desempenho o índice de acerto não chegou a 40%, o que mostra que o índice de erros foi maior que o de acertos para esses alunos. Segundo a Curva Característica do Item, os alunos cuja proficiência é próxima ou superior à média estadual apresentam maior probabilidade de responder corretamente essa tarefa do que incorretamente.
Dentre os distratores, chama a atenção o fato de as escolhas pelas alternativas (C) e (D), pois para essas medidas de hipotenusa sequer seria possível construir um triângulo, já que não atendem a condição de existência. Chama atenção também o fato de a alternativa (C) ser a segunda mais escolhida nos três Grupos de Desempenho, possivelmente por conjecturarem que a hipotenusa é igual a soma dos catetos. Não há mal algum em fazer conjecturas, porém é preciso averiguar sua validade, uma vez que é simples provar para o triângulo RST que não é verdade que a hipotenusa é igual a soma dos catetos.
Vale lembrar que as medidas 3, 4 e 5 para um triângulo correspondem a uma terna pitagórica recorrente em atividades, o que pode acabar favorecendo a escolha do 5 como opção de resposta. Ressalta-se também a situação estar atrelada a um fator de semelhança de fácil reconhecimento. Mediante isso, a proposição de novos cenários para estudo se mostra uma opção interessante para aprofundamento de estudos. Inclusive, sugere-se aqueles que utilizam números não inteiros como fator de semelhança, além de triângulos em posições diferentes, de modo a verificar se os estudantes são capazes de perceber a congruência entre os ângulos.
Um exemplo de proposta mais complexa, envolvendo semelhança, para determinação da medida do lado UV é a seguinte:

Por fim, é importante frisar as inúmeras possibilidades no estudo da semelhança de figuras planas, e não somente as triangulares, fornecendo aos estudantes um amplo rol de opções para estudo. |
 |
Exemplo 2
Nível Adequado
Compõe a descrição do ponto 325 da Escala de Matemática – SARESP

O item está atrelado a habilidade H32 – Calcular o volume de prismas em diferentes contextos – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o volume de prismas é tratado no 4º bimestre do 8º Ano do Ensino Fundamental. A tarefa proposta no item envolve a determinação do volume total de um cubo mágico, a partir da imagem desse cubo e que cada cubinho que o compõe possui volume de 1 cm3.
Nesse caso, a solução remete a uma das ideias primeiras para o cálculo de volume de prismas, a partição do sólido em cubos de volume unitário. Em outras palavras, trata-se de descobrir o número de cubinhos necessários para formar o sólido presente na imagem. Para tanto, pode-se particionar o cubo de diferentes maneiras, por exemplo:
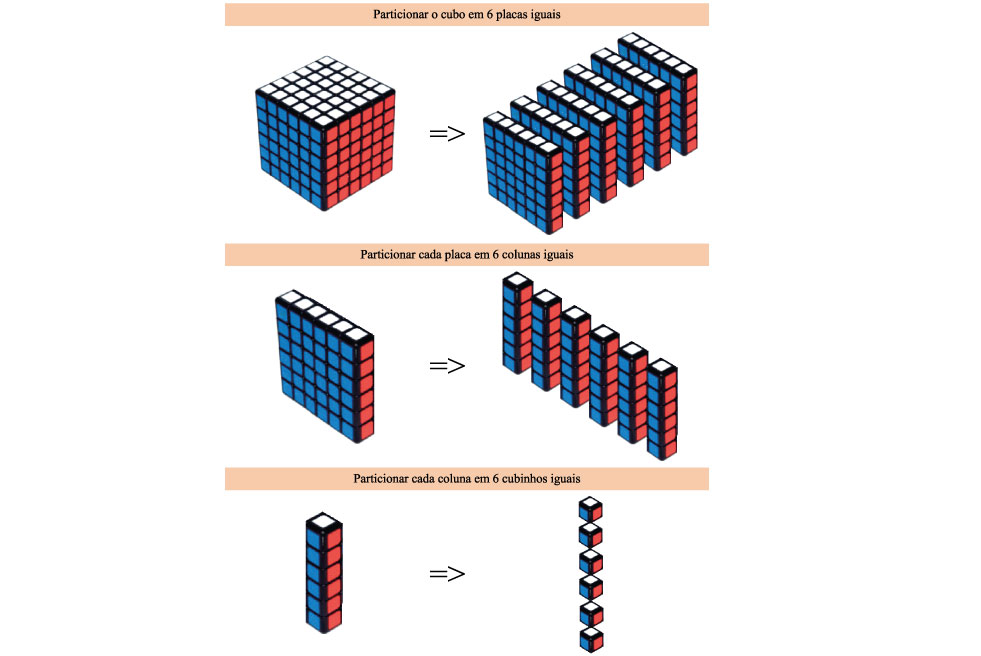
Portanto, cada cubo é formado por 6 placas, cada placa é composta por 6 colunas e cada coluna é feita a partir de 6 cubinhos. Logo, o cubo original possui 6 x 6 colunas ou 6 x 6 x 6 cubinhos, e como cada cubinho possui 1 cm3, o volume do cubo será igual a 216 cm3, ou seja, alternativa (D).
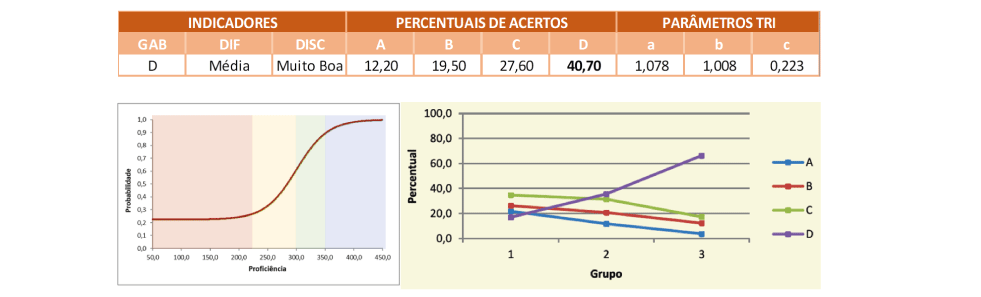
O item foi respondido corretamente por pouco mais de 40% dos estudantes, sendo que no Grupo de Menor Desempenho a alternativa correta foi a menos assinalada, enquanto que no Grupo Intermediário passou a ser a mais escolhida, porém por menos da metade dos alunos desse grupo, sendo que apenas no Grupo de Maior Desempenho o índice de acerto superou o índice de erro, sendo que quase dois terços desse grupo optaram pela alternativa correta.
A Curva Característica do Item mostra que para aqueles cuja proficiência é inferior à média estadual tem-se uma probabilidade de acerto muito próxima a de um acerto casual. Somente a partir do nível Adequado que a probabilidade de acerto supera 60% e apenas para o nível Avançado ultrapassa 80%.
Destaca-se que todos os distratores foram assinaladas por mais de 10% dos respondentes, sendo que o distrator (A) apresenta o número de faces do cubo, o distrator (B) refere-se ao número de cubinhos para uma placa, ou a área superficial de uma das faces, enquanto o distrator (C) traz o número de quadradinhos visíveis na imagem, o que também remete a área superficial, além de sugerir a ocorrência de uma confusão entre os conceitos de cubo e quadrado.
Vale ressaltar que a figura está em perspectiva, o que exige habilidade de compreensão desse tipo de representação por parte do alunado. Além disso, para esse cubo, em particular, o valor numérico do volume e da área superficial são iguais, o que implica na importância de verificar novas situações, envolvendo outros cubos ou prismas retangulares, tanto para verificar se os conceitos de volume e área superficial estão sendo assimilados corretamente como para reforçar a ideia de que figuras com áreas superficiais iguais podem ter volumes distintos, e vice-versa. |
 |
Exemplo 3
Nível Adequado
Compõe a descrição do ponto 325 da Escala de Matemática – SARESP

O item está atrelado a habilidade H17 – Resolver problemas que envolvam equações com coeficientes racionais – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o conceito de razão passa a ser tratado a partir do 7º Ano EF, enquanto a ideia de resolução de equação do 1º grau é tratada no 8º Ano EF. A tarefa proposta no item envolve a divisão de um serviço em duas partes não iguais, sendo que a razão do serviço atribuída a cada parte é dada por meio de fração.
Há diferentes meios de resolver esse problema, inclusive sem a necessidade de fazer uso da escrita de equações. Por exemplo, se na 1ª etapa 2/5 da estrada será asfaltada, então o restante, 3/5, será asfaltado na 2ª etapa. Com isso, a quantidade de asfalto na 2ª etapa será:
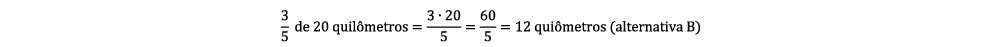
Vale destacar que a utilização de equações para modelar problemas precisa ser significativa para os estudantes, pois, do contrário, o uso dessa ferramenta será um dificultador a mais para obtenção da solução.
O uso de estimativa também é uma opção para obtenção da resposta correta. Para tanto, basta observar que:
- Se na 1ª etapa foi feito 2/5 do trabalho, então foi feito menos da metade, ou seja, sobrou mais de 10 quilômetros para a 2ª etapa. Essa informação permite excluir as alternativas (C) e (D).
- Ainda na 1ª etapa, a execução foi de 2/5 da estrada, ou seja, foi feito mais de 1/5 da obra e, portanto, mais do que 4 quilômetros (1/5 de 20 Km). Consequentemente, para a 2ª etapa da obra sobrou menos de 16 quilômetros de estrada para asfaltar. Com isso, exclui-se a alternativa (A)
- Por fim, na 2ª etapa a quantidade de asfalto que será feita é maior do que 10 quilômetros e menor do que 16, restando apenas a alternativa (B) como opção de resposta.
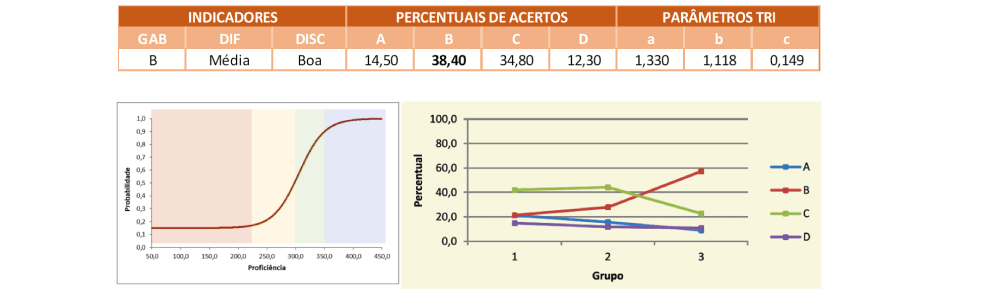
A alternativa correta foi assinalada por menos de 40% dos respondentes, sendo que a alternativa (C) teve um percentual de escolha muito próximo ao da alternativa correta, o que sugere que os alunos assumiram que a divisão do trabalho foi feita em duas etapas iguais, indicando uma leitura ineficiente para compreensão da situação. Pouco mais de 12% optaram pela alternativa (D) que apresenta a quilometragem asfaltada na 1ª etapa da obra, enquanto que quase 15% assinalou a alternativa (A) como resposta, sugerindo que, ao apontar 18 quilômetros como resposta, o respondente associou 2/5 da estrada com apenas 2 km, possivelmente por não reconhecer a fração como um meio de representar uma razão.
Segundo a Curva Característica do Item, apenas estudantes com nível de proficiência Adequado ou Avançado têm probabilidade de acerto superior a 50%, ou seja, somente 20,2% dos alunos da rede estadual tem maior chance de acerto do que de erro nessa tarefa. Já o quadro da distribuição de respostas por Grupo de Desempenho mostra que nos Grupos de Menor Desempenho e Intermediário predominou a ideia de que a divisão do trabalho foi feita de forma igualitária, sendo que apenas no Grupo de Maior Desempenho, a alternativa correta sobressaiu às demais.
Algumas variações do problema podem ser propostas, a fim de aprimorar o diagnóstico da situação. Por exemplo:
- A quebra do problema em etapas, por meio de perguntas.
- Nas etapas 1 e 2 será feita a mesma quilometragem de asfalto?
- Qual quilometragem corresponde a 1/5 da estrada?
- Se na 1ª etapa foi asfaltado 2/5 da estrada, qual fração restou para a 2ª etapa?
- Há proporcionalidade entre as razões 1/5, 2/5 e 3/5 da estrada?
- Qual equação modela esse problema?
- Verificar se a substituição da fração 2/5 por 40% modifica o entendimento da situação.
- Caso isso acontece, significa que o conceito de equivalência entre fração e porcentagem não foi devidamente assimilado.
- É preciso verificar se o uso da porcentagem não favorece o uso da regra de três sem a devida compreensão do que está sendo feito.
- Agregar um valor fixo de obra já realizado para deixar o problema mais complexo. Com isso, nova formulação pode ser sugerida: Um projeto de rodovia estava sendo desenvolvido quando foi paralisado por irregularidades. A obra previa a construção de 200 Km de rodovia, mas apenas 50 Km havia sido feito antes de uma paralisação. Agora, as obras serão retomadas em duas etapas, sendo que na 1ª etapa será realizado 2/5 da quilometragem ainda não feita, enquanto que na 2ª etapa será feito o restante.
Cabe ao professorado avaliar a viabilidade dessas variações, além de propor outras que atendam às necessidades e potencialidades de sua turma. |
 |
Exemplo 4
Nível Avançado
Compõe a descrição do ponto 350 da Escala de Matemática – SARESP
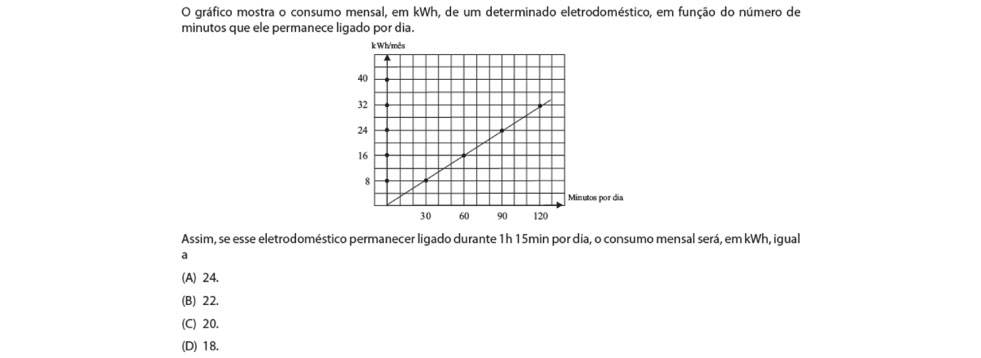
O item está atrelado a habilidade H20 – Resolver problemas envolvendo relações de proporcionalidade direta entre duas grandezas por meio de funções do 1º grau – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o assunto envolvido é pertinente a habilidades e expectativas do 2º bimestre do 9º Ano do Ensino Fundamental. A tarefa proposta no item envolve a leitura de um gráfico de uma função do 1º grau, que relaciona o número de minutos que um aparelho fica ligado diariamente e o consumo de energia mensal que isso acarreta, para determinar o consumo mensal desse aparelho se ele ficar ligado por 1 hora e 15 minutos.
Para resolver corretamente o problema é necessário observar que o gráfico apresenta o tempo de funcionamento em minutos, logo é preciso transformar 1 hora e 15 minutos em 75 minutos. Com isso, percebe-se que a resposta não pode ser obtida por meio de uma leitura direta do gráfico, uma vez que esse tempo não se encontra em destaque no eixo horizontal. O gráfico permite apenas afirmar que para 75 minutos, o consumo fica compreendido entre 16 kWh e 24 kWh por mês, valores respectivos a 60 e 90 minutos.
O fato de o gráfico conter a origem do plano cartesiano implica em afirmar que se trata de um caso particular da função de 1º grau, chamada função linear. Para esse caso, há a garantia da existência de proporcionalidade entre as grandezas envolvidas e, a partir disso, é possível obter o consumo desse eletrodoméstico a partir de algum dado retirado do gráfico. Por exemplo, se utilizarmos que 30 minutos diários do aparelho acarretam em um consumo mensal de 8 kWh, então para 1 hora e 15 minutos (75 minutos) tem-se que:

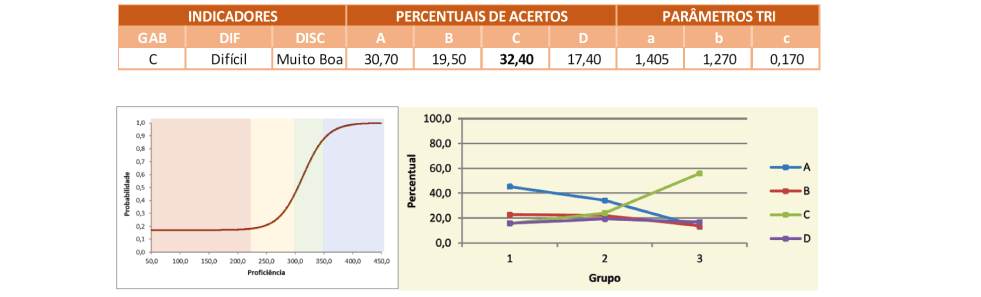
A alternativa correta foi assinalada por pouco menos de um terço dos respondentes, indicando um item difícil na percepção dos estudantes. Chama a atenção o fato de a alternativa (A) ter tido um percentual de escolha muito próximo da alternativa correta. A escolha dessa alternativa por um número significativo de alunos acarreta certa estranheza, pois é a única alternativa apresentada diretamente no gráfico e que, ao localizá-la, percebe-se sua correspondência com o tempo de 90 minutos, que não equivale a 1 hora e 15 minutos. Isso também pode sugerir a necessidade de o aluno encontrar a resposta via leitura direta do gráfico, demonstrando não compreender a ideia de continuidade da reta, que caracteriza o traço da função. Já as alternativas (B) e (D) juntas correspondem a praticamente 37% das repostas observadas e são oriundas possivelmente por erros de cálculos ou percepções visuais imprecisas da representação gráfica.
A Curva Característica do Item reforça a complexidade do problema, pois mostra que para alunos no nível Abaixo do Básico ou Básico, ou seja 71,5% do alunado paulista, a probabilidade de responder corretamente esse problema é inferior a chance de fazê-lo de forma incorreta. Isso mostra que o domínio dessa habilidade exige a capacidade de mobilizar conhecimentos mais complexos, ainda não plenamente desenvolvidos no Ensino Fundamental e que serão retomados no Ensino Médio, o que está alinhado com um item de nível Avançado.
Frente ao exposto, recomenda-se a análise de novas situações envolvendo funções lineares para uma melhor avaliação do entendimento dos alunos sobre a temática. Além do mais, caso o professor entenda ser possível, trazer situações modeladas por funções afins que não apresentam proporção direta entre as grandezas, devida a presença do coeficiente linear não nulo. Esse tipo de trabalho, além de aprimorar a concepção dos estudantes, certamente contribuirá para o estudo aprofundado de funções no Ensino Médio. |
|
|
|

|
