|
|
 |
A edição 2019 do SARESP aferiu a proficiência dos estudantes do 7º Ano do Ensino Fundamental, sendo que a média obtida foi igual a 237,7. Esse valor indica um nível de proficiência classificado como Básico para a turma em questão. Destaca-se, nesse ano escolar, a retomada do crescimento na média estadual, motivada principalmente pelo aumento de alunos nos níveis Adequado e Avançado, que, nessa edição, corresponde a 39,0% do alunado paulista. Assim, praticamente 4 em cada 10 alunos da rede demonstraram ter domínio pleno ou acima das competências esperadas para o ano escolar em questão.
A seguir, são apresentados exemplos comentados a fim de ilustrar atividades características que os alunos foram capazes de realizar ou que demonstraram dificuldades. Além do enunciado e da solução dos itens, há a indicação de alternativas de trabalho, além de uma representação gráfica da frequência de escolha de cada alternativa nos três Grupos de Desempenho e a Curva Característica do Item que associa a proficiência do respondente e a probabilidade de acertar a questão.
Exemplo 1
Nível Básico
Compõe a descrição do ponto 200 da Escala de Matemática – SARESP

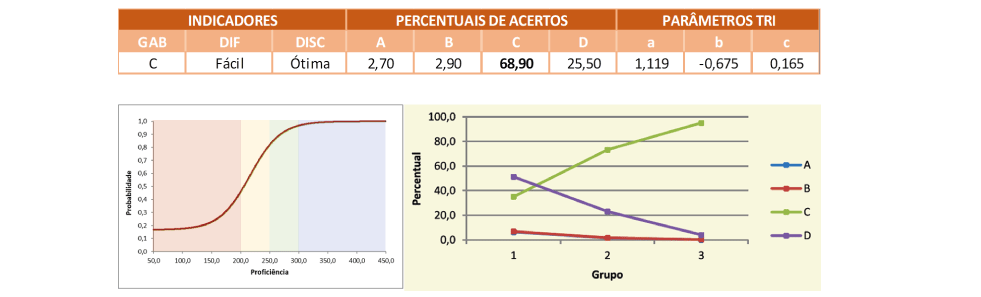
O item está atrelado a habilidade H07 – Fazer cálculos que envolvam adições e subtrações de números decimais – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o assunto está atrelado a habilidades propostas para os dois primeiros bimestres do 6º Ano do Ensino Fundamental e para o 1º bimestre do 7º Ano EF. A tarefa apresenta, apesar de estar atrelada a uma situação-problema, deixa evidenciado o cálculo que precisa ser realizado. Logo, basta resolver 100,00 – 90,25, da maneira que for mais familiar para o alunado, para obtenção da resposta. A seguir, são apresentadas duas soluções, uma correta e uma incorreta, que partem da mesma conta armada:
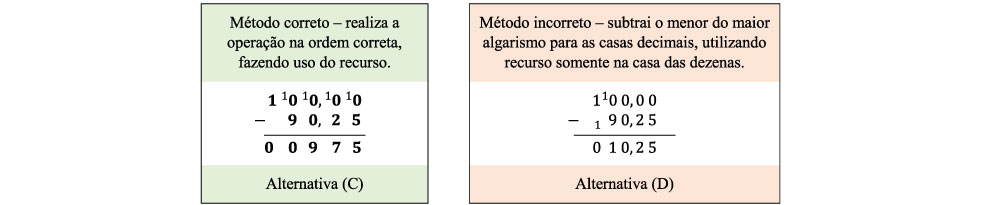
Interessante observar que o erro apresentado acima está ligado a uma ideia de subtrair o menor do maior algarismo, independentemente da ordem apresentada no cálculo. Esse tipo de equívoco deixou de ser recorrente nas provas do 3º ano EF em subtrações envolvendo números naturais, porém parece estar sendo cometido no cálculo entre números decimais. Com isso, reitera-se a necessidade de o professor estar atento as técnicas e, principalmente, as ideias empregadas pelos estudantes na resolução de contas envolvendo diferentes conjuntos numéricos.
A estimativa também se mostra uma opção interessante para resolver esse tipo de problema. Nesse caso, bastaria o estudante atentar-se que o valor subtraído é superior a R$90,00 e inferior a R$91,00. Com isso, o troco deve estar compreendido entre a subtração de R$100,00 e os valores apresentados anteriormente, ou seja, o troco é um valor entre R$10,00 e R$9,00, o que restringe apenas a alternativa (C) como opção válida de resposta.
O item foi acertado por pouco mais de dois terços dos respondentes que participaram do teste, sendo que para os alunos do Grupo de Maior Desempenho esse percentual atinge 95% enquanto que para o Grupo de Menor Desempenho o índice de acerto é de apenas 35%, o que caracteriza um item com ótima capacidade de discriminação.
A Curva Característica do Item mostra que alunos cujo nível de proficiência é classificado como Abaixo do Básico tem, no máximo, 45% de chance de resolver corretamente esse tipo de questão, já para alunos no nível Básico, a probabilidade de acerto varia de 45% a pouco mais de 80%, enquanto que os estudantes cuja proficiência é Adequada ou Avançada apresenta altíssima chance de responder corretamente esse tipo de tarefa.
Como meio de tornar a tarefa mais complexa, também poderia ser solicitado ao alunado estimar o valor pago por litro de combustível (ideia atrelada a divisão), assim como determinar a quantidade de litros abastecidos para outra quantia em reais paga (ideia atrelada a proporção). Claro, cabe ao professor responsável averiguar a necessidade de adequar os números apresentados na questão, de modo a construir um cenário mais condizente com sua turma.
Na prova do 5º Ano EF foi proposta uma tarefa também atrelada a subtração entre decimais, porém mais complexa, no formato de resolução de problema, na qual era solicitado a diferença entre os pesos de duas embalagens, sendo que uma continha 1,1 Kg do produto enquanto a outra tinha 1,010 Kg. Esse tipo de situação também é altamente recomendado aqui, já que no 5º Ano EF menos da metade dos respondentes se mostrou capaz de obter a resposta correta.
|
 |
Exemplo 2
Nível Adequado
Compõe a descrição do ponto 250 da Escala de Matemática – SARESP
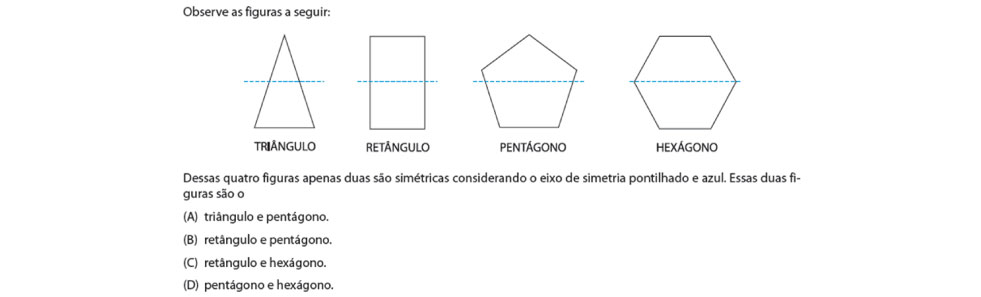
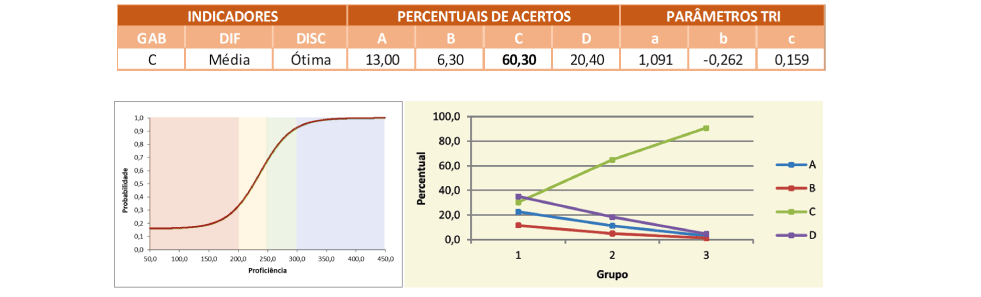
O item está atrelado a habilidade H20 – Identificar simetria axial e de rotação na leitura das representações dos objetos no dia a dia e das figuras geométricas – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o assunto está relacionado a habilidades previstas para o 3º bimestre do 6º Ano e para o 2º bimestre do 7º Ano do Ensino Fundamental. A tarefa proposta no item envolve o reconhecimento de figuras geométricas simétricas, a partir de um eixo de simetria horizontal.
A solução desse exercício pode ser obtida de diferentes maneiras, sendo que uma delas consiste em dividir as figuras no eixo de simetria apresentado e analisar ser as metades obtidas são iguais ou não. A ilustração a seguir mostra essa ideia, observe:

Note que apenas o retângulo e o hexágono quando divididos apresentam formas equivalentes. Se mesmo assim a dúvida persistir, pode-se refletir a peça superior para nova comparação com a peça inferior. Veja:

Nesse caso, fica ainda mais evidenciada a semelhança para o retângulo e para o hexágono. Ainda, se necessário, o estudante poderá sobrepor as imagens superior e inferior, conforme ilustrado a seguir:

Observe que as formas superior e inferior para o triângulo e para o pentágono não se sobrepõem. Logo, elas não apresentam simetria. Sendo assim, apenas o retângulo e o hexágono apresentam simetria, de acordo com o eixo proposto.
A alternativa correta (C) foi a opção de resposta de 6 em cada 10 alunos que resolveram esse item, indicando que esse tipo de cenário é conhecido pela maioria dos estudantes. De toda forma, no Grupo de Menor Desempenho ainda há trabalho a ser realizado, uma vez que a alternativa mais assinalada nesse Grupo de respondentes foi a (D), indicando que o pentágono e o hexágono eram as figuras simétricas, segundo o eixo proposto.
Com relação aos distratores é importante frisar que todas as figuras apresentadas seriam simétricas se o eixo proposto estivesse na vertical, conforme a figura abaixo:

Contudo, o comando é claro ao referir-se ao eixo de simetria pontilhado e azul, de modo que a simetria apresentada acima não pode ser considerada para obtenção da resposta.
A Curva Característica do Item mostra que os estudantes que apresentam proficiência próxima a média estadual tem probabilidade de acerto de aproximadamente 55%, ou seja, apresentam leve vantagem na chance de acerto para esse item. Somente para alunos do nível Avançado a probabilidade de resolver corretamente esse tipo de tarefa é superior a 90%.
Importante destacar que o item pode ser adaptado, oferecendo outros eixos de simetria ou mesmo novas formas geométricas. Além do mais, é possível explorar também a simetria por rotação. Frente a isso, cabe perguntar: Quais das figuras propostas no exemplo apresentam simetria de rotação? O ângulo de rotação é o mesmo para todas as figuras? Se sim, qual ângulo é esse? Caso não, quais são os ângulos de simetria para cada figura?
|
 |
Exemplo 3
Nível Adequado
Compõe a descrição do ponto 275 da Escala de Matemática – SARESP
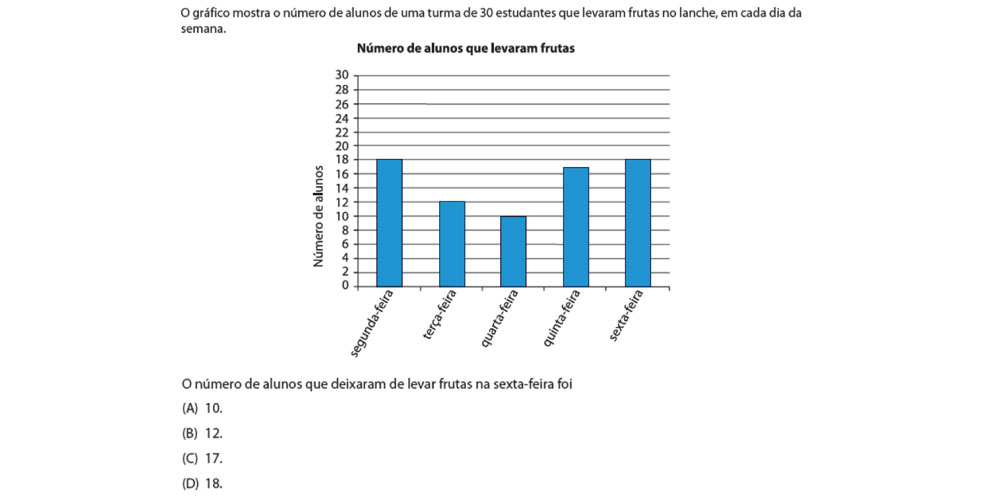
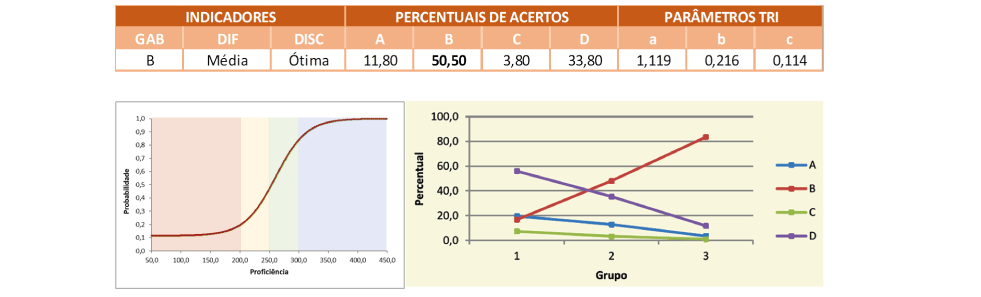
O item está atrelado a habilidade H35 – Identificar e interpretar informações transmitidas por meio de gráficos – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o assunto está relacionado a habilidades previstas no 4º bimestre do 6º Ano do Ensino Fundamental. A tarefa proposta no item envolve uma interpretação não usual de um gráfico de colunas, pois recorre a leitura do gráfico para obtenção do número de alunos que levaram frutas no lanche para então determinar o número de alunos que não levaram, a partir do número total de alunos dessa turma.

A solução pode ser ilustrada graficamente, uma vez que o valor máximo do eixo vertical é exatamente o número de alunos da turma. Desse modo, o gráfico pode ser lido da seguinte maneira:
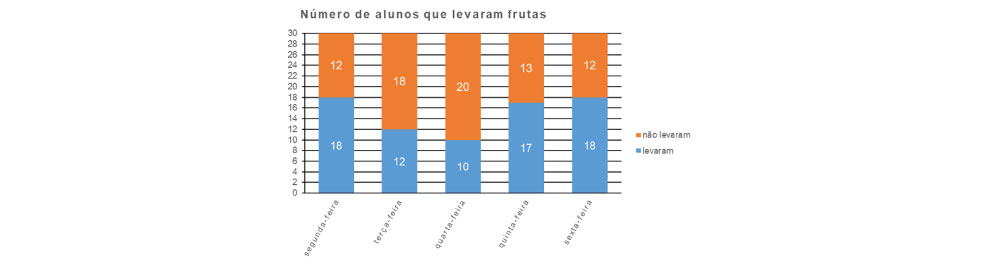
A partir desse novo gráfico é possível identificar que 12 alunos não levaram fruta na sexta-feira (alternativa B). Essa resposta foi a assinalada por pouco mais de 50% dos respondentes, ou seja, praticamente 1 em cada 2 estudantes não soube resolver a tarefa proposta. Destaca-se a grande diferença entre o índice de acerto para os Grupos de Menor (16,8%) e Maior (83,6%) Desempenho, o que caracteriza um item com ótima discriminação. Além disso, somente no Grupo de Maior Desempenho que o número de alunos que respondeu corretamente o problema supera os que erraram.
Dentre os distratores, a alternativa (D) foi escolhida por um terço dos respondentes. A escolha dessa alternativa possivelmente se deve ao fato de ela apresentar o número de alunos que levaram fruta na sexta-feira, indicando desatenção na leitura do enunciado e na execução da tarefa. Outro contingente significativo de estudantes optou pela alternativa (A), cujo valor apresentado está atrelado ao dia que menos alunos levaram fruta, sugerindo uma possível interpretação errônea do comando.
A Curva Característica do Item mostra que alunos cuja proficiência está no Abaixo do básico tem probabilidade de acerto pouco superior à do acerto casual. Além disso, mesmo alunos com proficiência Básica possuem maior chance de responder incorretamente esse tipo de tarefa. Somente para alunos do nível Adequado e, principalmente, do Avançado que a probabilidade de acerto supera a chance de resolver errado essa tarefa.
Explorar as informações contidas em um gráfico implica em várias possibilidades de análise. Ser capaz de realizar diferentes análises é parte fundamental para o desenvolvimento pleno das habilidades atreladas ao estudo de gráficos e tabelas.
Seguem algumas sugestões para o gráfico do problema:
- Quais dias um mesmo número de alunos levou frutas?
- Quanto deve resultar a soma dos alunos que levaram e dos que não levaram fruta?
- Qual dia um maior número de alunos deixou de levar fruta?
- Há outros modelos de gráficos que podem ser utilizados para representar esses dados?
- Porque um gráfico de setores não pode ser utilizado para apresentar esses dados?
|
 |
Exemplo 4:
Nível Avançado
Compõe a descrição do ponto 325 da Escala de Matemática – SARESP

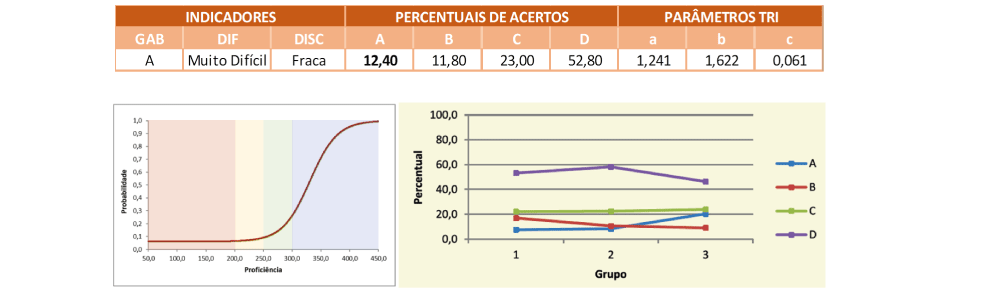
O item está atrelado a habilidade H38 – Resolver problemas que envolvam a ideia do princípio multiplicativo de contagem – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o assunto está relacionado a uma habilidade prevista para o 4º bimestre do 6º Ano do Ensino Fundamental. A tarefa proposta no item envolve determinar de quantas maneiras distintas uma pessoa poderá escolher três figurinhas para entregar para um amigo, sob determinadas condições.
Nesse caso, é preciso destacar que cada figurinha escolhida deverá ser de uma seleção de futebol, sendo que há 6 figurinhas do Brasil, 4 da Alemanha e 7 do Egito. A ideia de escolher uma, e apenas uma, figurinha dentre as disponíveis para cada seleção é o que caracteriza a ideia do princípio multiplicativo. Consequentemente, o número total de trincas de figurinhas distintas que poderão ser escolhidas com as figurinhas disponíveis é dado pelo produto do número de figurinhas disponíveis para cada seleção, ou seja:
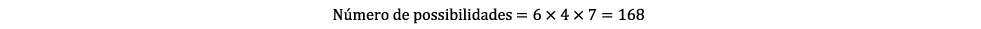
O item, classificado como muito difícil, foi acertado por 12,4% dos respondentes, o que corresponde a aproximadamente 1 acerto a cada 8 alunos que tentaram resolver esse problema. A alternativa correta (A) foi uma das menos assinaladas em todos os Grupos de Desempenho, o que implica em uma discriminação fraca, já que a grande maioria dos alunos demostrou dificuldade frente a esse tipo de situação.
Dentre os distratores, a alternativa (D), que apresenta a soma do número de figurinhas disponíveis para cada seleção, foi escolhida por mais da metade do alunado. A alternativa (C) foi escolhida por quase um quarto dos respondentes, possivelmente por ser um valor próximo ao triplo da soma das figurinhas disponíveis, caracterizando a escolha de uma estratégia que utiliza os números do enunciado, mas que não possui validade matemática.
A Curva Característica do Item mostra um item complexo que requer alta proficiência para ser respondido corretamente. Mesmo no início do nível avançado (ponto 300) a probabilidade de acerto não ultrapassa 30%.
Curiosamente, o problema apresentado acima é muito similar a outro discutido na Revista Eletrônica 2018. Ambos os problemas envolviam a escolha de três itens, sendo que cada item apresentava um rol de opções para a escolha de uma e apenas uma delas. O item de 2018 era o seguinte:

Tanto no problema proposto em 2018 como o apresentado em 2019 o número de respondentes que opta pela somatória das possibilidades de escolha para cada item é consideravelmente alta, sendo maior em 2019 do que em 2018. Isso levanta alguns questionamentos sobre a maior complexidade percebida na edição atual:
- Os alunos percebem que há um paralelismo entre escolher três peças distintas de roupas e três figurinhas de diferentes seleções?
- Os números envolvidos no cálculo geraram um resultado aparentemente grande (168) que fez com que os alunos estranhassem tamanho número de opções de escolha para apenas três figurinhas? Ou teria sido o cenário/contexto que dificultou a compreensão do problema?
- Como evitar que a ideia de somar o número de opções deixe de ser uma estratégia de solução utilizada pelos estudantes?
Propor diferentes casos para estudo se mostra uma demanda urgente e necessária para a busca em reverter esse cenário.
|
|
|
|

|
