|
|
 |
A edição 2019 do SARESP aferiu a proficiência dos estudantes do 5º Ano do Ensino Fundamental, sendo que a média obtida foi igual a 231,3. Esse valor indica um nível de proficiência classificado como Adequado para a turma em questão. Destaca-se, nesse ano escolar, a crescente das médias ao longo dos últimos anos, caracterizada não somente pelo aumento da média estadual para essa turma, mas principalmente pela migração de alunos dos níveis de proficiência mais baixos para níveis superiores. Em relação a isso, cabe apontar que apenas 14,0% dos alunos da rede foram classificados no nível Abaixo do Básico, enquanto que 20,0% estão no nível Avançado. A seguir, são apresentados exemplos comentados a fim de ilustrar atividades características que os alunos foram capazes de realizar ou que demonstraram dificuldades. Além do enunciado e da solução dos itens, há a indicação de alternativas de trabalho, além de uma representação gráfica da frequência de escolha de cada alternativa nos três Grupos de Desempenho e a Curva Característica do Item que associa a proficiência do respondente e a probabilidade de acertar a questão.
Exemplo 1
Nível Básico
Compõe a descrição do ponto 175 da Escala de Matemática – SARESP


O item está atrelado a habilidade H01 – Identificar a localização de números naturais na reta numérica – segundo a Matriz de Referência de Avaliação do SARESP, sendo que para o 5º Ano do Ensino Fundamental tem-se como expectativa de aprendizagem a comparação e ordenação de números racionais, na representação fracionária e na representação decimal, localizando-os na reta numérica. Ou seja, a tarefa proposta no item se mostra menos complexa do que essa expectativa de aprendizagem, pois envolve a localização de números naturais, identificando entre quais dois números apresentados numa reta numérica está posicionado o número 153.
Uma maneira de resolver o problema proposto envolve observar os números dispostos na reta numérica, nesse caso: 125, 145, 165, 185, 205 e 225. A partir desses é possível compará-los para determinar quais são menores e quais são maiores que o número 153. Por fim, é necessário observar que o 153 é maior que o número 145 e menor que o número 165 e, portanto, está localizado entre esses dois números, ou seja, alternativa (B). Outro caminho para obtenção da solução está em analisar qual dos números presentes na reta numérica está mais próximo do 153, sendo que se o número 153 for maior que esse número mais próximo ele ficará posicionado à direita desse número, enquanto que se for menor deverá estar à esquerda. Um detalhe importante é que uma leitura cuidadosa da reta numérica permite perceber que os números crescem conforme desloca-se à direita na reta numérica.
A alternativa correta foi assinalada por 87,5% dos respondentes, sendo a opção de resposta mais escolhida em todos os Grupos de Desempenho. Aqueles que optaram pela alternativa (A) possivelmente utilizaram o número 145 como referência, mas enganaram-se no sentido da reta, colocando o número 153 à esquerda do 145. De modo semelhante, aqueles que optaram pela alternativa (C) podem ter utilizado o número 165 como referências, porém colocaram equivocadamente o número 153 à direita, ao invés de à esquerda, desse número. Por fim, apenas 2,2% dos respondentes optaram pela alternativa (D) e, para esses, é necessário direcionar um olhar mais atento, já que essa opção de resposta apresenta apenas valores maiores que o 153, não possibilitando que ele esteja posicionado entre esses valores.
A Curva Característica do Item mostra que o alto índice de acerto era esperado, uma vez que os estudantes que possuem proficiência próxima a média estadual apresentam alta chance de responder corretamente essa tarefa. Frente a isso, vale ressaltar a possibilidade de propor novas tarefas relacionadas a habilidade em questão. Por exemplo, variar a graduação da reta é uma alternativa interessante, para que o estudante busque fazer novas comparações.
A seguir são apresentadas três sugestões de retas com novas marcações para a localização do número 153:

Aliás, para alunos com níveis mais altos de proficiência pode-se propor o desafio de apresentar a posição do número 153, buscando respeitar o distanciamento entre os números e a escala proposta em cada reta numérica.
|
 |
Exemplo 2
Nível Adequado
Compõe a descrição do ponto 225 da Escala de Matemática – SARESP

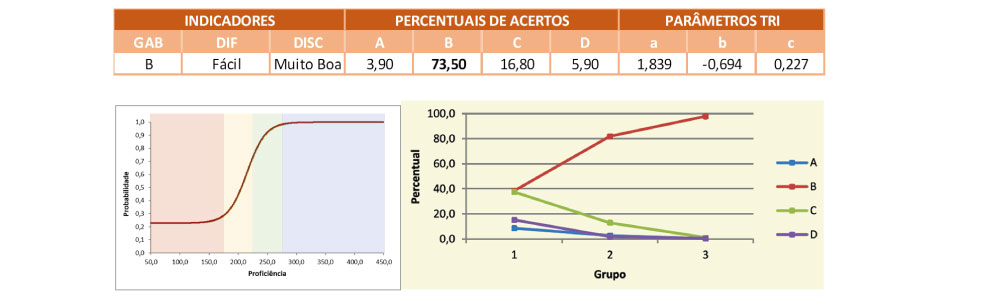
O item está atrelado a habilidade H16 – Resolver problemas que envolvam noções de porcentagem – segundo a Matriz de Referência de Avaliação do SARESP, sendo que a tarefa proposta nesse item é uma das expectativas de aprendizagem para o 5º Ano do Ensino Fundamental. O problema apresentado envolve quantificar 50% de uma turma de alunos, percentual que representa o número de meninas na sala. Uma opção de estratégia de solução seria associar 50% à metade da turma, ou seja, das 30 crianças que compõem a turma, metade (50%) são meninas, ou seja, nessa turma temos 15 meninas, alternativa (B).
O problema foi respondido corretamente por 73,5% dos respondentes, ou seja, praticamente um em cada quatro estudantes que resolveram esse item não soube associar 50% à metade do todo e/ou não conseguiu calcular a metade de 30, o que sugere que uma parte considerável do alunado não atingiu a expectativa prevista para o ano em questão. Dos distratores, a alternativa (C) foi a mais escolhida, possivelmente devido a alguma relação direta e errônea entre os números 30 e 50 estabelecida pelos respondentes, já que a diferença entre os números é igual a 20.
Compreender a ideia de porcentagem como uma razão ou comparação é fundamental para o desenvolvimento pleno do conceito, inclusive para que a temática não se torne um apanhado de técnicas de cálculo sem significado para os estudantes. Frente a isso, algumas porcentagens podem ser trabalhadas em um primeiro momento. São elas:
100% – corresponde a totalidade da quantidade analisada e, por isso, quando se usa porcentagem para representar a parte de um todo, como no caso do problema apresentado, o percentual atrelado a essa parte nunca pode ser superior a 100%.
50% – representa a ideia de metade do todo, independentemente da quantidade desse todo. Ou seja, 50% sempre representa a metade da quantidade total, seja de um tanque de combustível de um carro, de uma xícara de farinha para uma receita, de pessoas presentes em uma reunião. Nesses exemplos, 20 litros de um tanque, 100 gramas de farinha e 15 pessoas em uma reunião representam 50% da totalidade, mesmo que a quantidade obtida em cada situação seja diferente.
25% – está atrelado a um quarto do todo ou, simplesmente, metade da metade do todo, ou seja metade de 50%. Assim, para obter essa porcentagem de uma quantidade basta dividi-la ao meio duas vezes.
10% – corresponde a um décimo do todo, sendo obtido a partir da divisão do todo por 10.
1% – analogamente, corresponde a um centésimo do todo, sendo obtido a partir da divisão do todo por 100. A depender das potencialidades da turma de estudantes, para as discussões iniciais envolvendo as observações feitas acima será necessário trabalhar com quantidades que permitam uma divisão de resultado exato, sem resto.
Vale trazer junto aos alunos que é possível obter novas porcentagens a partir das já conhecidas. Por exemplo, é possível calcular 12% de um todo utilizando os valores de 10% e 1%, numa ideia semelhante a decomposição numérica, fazendo: 12% = 10% + 1% + 1%.
Outra possibilidade de trabalho na sala de aula envolve o processo inverso, ou seja, determinar a porcentagem que a parte do todo representa. Nesse caso, o problema poderia ser apresentado da seguinte forma:
A turma do 5º ano da professora Márcia poucos vieram de agasalho. Na sala há 30 crianças, sendo que apenas 6 delas estão agasalhadas. Qual o percentual de crianças na sala da professora Márcia agasalhadas? Aproveite e informe qual o percentual de crianças sem agasalho. Nesse cenário, ao dividir 30 (todo) por 6 (agasalhadas) obtemos 5 como resposta. Com isso, pode-se afirmar que o número de crianças agasalhadas corresponde a 1/5 do total de crianças e, portanto, pode ser representado por 1/5 de 100%, que é igual a 100% dividido por 5, resultando em 20%. Consequentemente, os alunos sem agasalhos podem ser representados pela porcentagem que falta para totalizar 100%, ou seja, 80%. Essa última afirmação pode parecer simples, mas requer domínio da temática, além da percepção de que a situação apresentada é dicotômica: ou a criança está agasalhada ou não está.
Promover esse tipo de aprofundamento, quando possível, favorece a compreensão de problemas mais complexos que serão apresentados em anos posteriores para o alunado, contribuindo com o trabalho dos futuros professores desses estudantes. Vale destacar, por exemplo, que na prova do 7º Ano do Ensino Fundamental apenas pouco mais de um quarto dos respondentes foram capazes de associar 20% de bateria restante de um celular com 1/5 da capacidade total da bateria.
|
 |
Exemplo 3
Nível Adequado
Compõe a descrição do ponto 225 da Escala de Matemática – SARESP

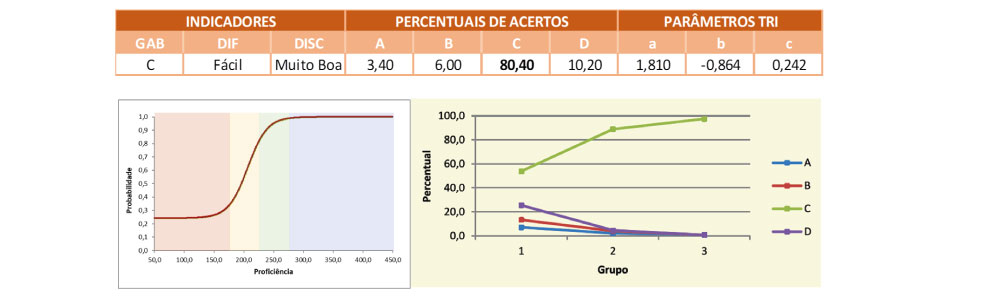
O item está atrelado a habilidade H21 – Identificar horas e minutos, por meio da leitura de relógios digitais e de ponteiros – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o assunto é tratado no já no 2º Ano do Ensino Fundamental. A tarefa proposta no item envolve uma leitura comum do dia a dia para um relógio digital, na qual, ao invés de se informado as horas e os minutos apresentados no relógio, é dado quantos minutos faltam para determinada hora, o que implica em uma tarefa que se mostra mais complexa do que a simples leitura do horário apresentado em um relógio digital.
A solução desse problema pode ser obtida a partir da análise dos dados presentes no enunciado. O fato de se encontrarem poucos minutos antes das 20 horas implica que o horário de encontro deve ser o das 19 horas e alguns minutos. Nesse caso, como 1 hora corresponde a 60 minutos, então 10 minutos antes implica em 19h50, a alternativa (C).
Vale destacar que pouco mais de 13% dos respondentes optaram pelas alternativas (A) ou (D) e, portanto, não reconheceram que o horário de encontro devem ser o das 19 horas e alguns minutos. Além desses, outros 6% associaram o tempo de 10 minutos anterior ao início do filme com a hora anterior mais 10 minutos, respondendo 19:10 (alternativa B). Já os demais alunos, praticamente 80% dos respondentes, identificaram o horário correto do encontro de Eliana e Márcia.
A alternativa correta foi a mais assinalada nos três Grupos de Desempenho, sendo que no Grupo de Maior Desempenho, o índice de acerto foi de quase 98%. A Curva Característica do Item mostra que os alunos do nível Abaixo do Básico têm maior chance de responder incorretamente essa questão. Já os do nível Básico apresentam chance de acerto variando de 35% a 85% conforme aumenta a proficiência. Já os estudantes dos níveis Adequado e Avançado têm altíssima probabilidade de responder corretamente esse tipo de tarefa.
Vale destacar que a situação poderia ser apresentada com a expressão “8 horas da noite” ao invés de “20h” conforme consta no enunciado do problema. Além disso, a utilização de relógios de ponteiros nas alternativas, no lugar de relógios digitais, também poderia ser pensada a fim de aumentar a complexidade do problema proposto.
Por fim, ressalta-se que para outro problema, semelhante a esse, no qual o horário informado era 25 minutos antes da hora exata, foi observada um comportamento muito similar dos estudantes, sugerindo que não é quantidade de minutos que envolvido no problema que tem feito os respondentes optarem por uma das alternativas incorreta. |
 |
|
|
|
 |
|
