|
|
 |
1. A MATEMÁTICA NO 3º ANO DO ENSINO FUNDAMENTAL
O objetivo do relatório da 22ª edição do SARESP (Sistema de Avaliação do Rendimento Escolar do Estado de São Paulo) é apresentar aos profissionais da Educação o desempenho dos alunos do 3º ano do Ensino Fundamental na prova de Matemática do SARESP, edição 2019.
As provas aplicadas foram elaboradas de acordo com um conjunto de habilidades contempladas nas orientações e recomendações didático-pedagógicas da Secretaria da Educação do Estado de São Paulo.
A prova, apresentada nas versões manhã e tarde, seguiu os padrões e procedimentos das edições anteriores, tendo como novidade a aplicação também para o 2º ano, com algumas questões selecionadas e, em alguns casos adaptadas, da prova do 3º ano.
Coube a um professor aplicador ler as questões da prova aos alunos, seguindo as orientações descritas no Manual do Aplicador e no Caderno de Prova do Professor, que enfatizavam a necessidade de não fornecer indícios para a solução dos problemas lidos.
Após a aplicação, as provas foram recolhidas e digitalizadas para a realização do processo de correção online das questões. Ao todo 220 professores foram supervisionados e capacitados por 11 supervisores, além de 2 coordenadores gerais de área, para o cumprimento do processo de correção das provas de Matemática.
1.1. CARACTERÍSTICAS DAS PROVAS DE MATEMÁTICA DO 3º ANO DO ENSINO FUNDAMENTAL – SARESP 2019
As provas para os alunos do 3º ano do Ensino Fundamental foram elaboradas no intuito de avaliar as habilidades dos alunos nos diferentes objetos do conhecimento da Matemática: números e operações, espaço e forma, grandezas e medidas e, tratamento da informação.
Foram contempladas, tanto nas provas da manhã como nas da tarde, as mesmas habilidades nos itens de resposta construída, ordenadas em uma mesma sequência de aplicação, e visavam propor situações-problema contextualizadas para os alunos. Continham 13 itens de resposta construída, sendo 3 com duas perguntas, além de outros 5 itens de múltipla escolha, que contemplaram habilidades distintas para manhã e tarde, ainda que com níveis de dificuldade equivalentes.
Destaca-se a similaridade entre as 13 questões de resposta construída das provas dos dois períodos, pois possuíam o propósito de avaliar as mesmas habilidades. As diferenças entre as provas estavam apenas nos números envolvidos, porém sempre com a preocupação de que possuíssem a mesma magnitude e contexto.
1.2. MATRIZ DE REFERÊNCIA DE AVALIAÇÃO DE MATEMÁTICA - 3º ANO DO ENSINO FUNDAMENTAL
Para as provas de Matemática apresentadas ao 3º ano do Ensino Fundamental no SARESP 2019, as questões foram elaboradas e selecionadas para investigar as habilidades descritas no quadro a seguir:.
Quadro 1 – Descrição das habilidades da prova SARESP 2019 – Matemática – 3º Ano do Ensino Fundamental

1.3. CORREÇÃO E RESULTADOS DAS PROVAS DO 3º ANO DO ENSINO FUNDAMENTAL - SARESP 2019
A correção e o processo de codificação da prova foram realizados online, segundo metodologia desenvolvida pela VUNESP, empregada desde 2013. Nesse processo, após treinamento inicial, cada questão foi apresentada isoladamente aos corretores, sendo corrigida e pontuada de acordo com as categorias de respostas previamente definidas. As questões passaram por duas correções e em caso de discrepância entre elas, foram encaminhadas para a terceira correção.
O quadro a seguir descreve, de modo geral, as categorias dos itens de resposta construída pelo aluno, da avaliação de Matemática do 3º ano do Ensino Fundamental, no SARESP 2019.
Quadro 2 – Descrição dos itens e distribuição percentual dos alunos do 3º ano do Ensino Fundamental, segundo as categorias de resposta – SARESP 2019 – Matemática – Manhã e Tarde

O quadro seguinte descreve os itens de múltipla escolha, seus respectivos gabaritos e o percentual de acerto dos alunos na avaliação de Matemática do 3º ano do Ensino Fundamental, no SARESP 2018, provas manhã (M) e tarde (T).
Quadro 3 – Descrição dos itens e distribuição percentual dos alunos do 3º ano do Ensino Fundamental para os itens de múltipla escolha – SARESP 2019 – Matemática – Manhã (M) e Tarde (T)

2. RESULTADOS DA ANÁLISE ESTATÍSTICA DOS ITENS DA PROVA DE MATEMÁTICA DO 3º ANO DO ENSINO FUNDAMENTAL DO SARESP 2019
O processamento estatístico pela Teoria da Resposta ao Item (TRI), dos resultados da correção das questões da prova de Matemática do 3º ano do Ensino Fundamental forneceu a posição dos itens na escala do SARESP. Para obtenção das estimativas dos parâmetros dos itens de resposta construída e das proficiências representados pelo Modelo de Resposta Gradual foi utilizado o software IRTPro 2.1. Considerando os intervalos que delimitam os níveis de proficiência do SARESP para Matemática no 3º Ano do Ensino Fundamental, a tabela abaixo inclui o posicionamento dos itens segundo os níveis de proficiência em que se ancoram.
Tabela 1 – Posicionamento dos itens de resposta construída na escala de proficiência – SARESP 2019
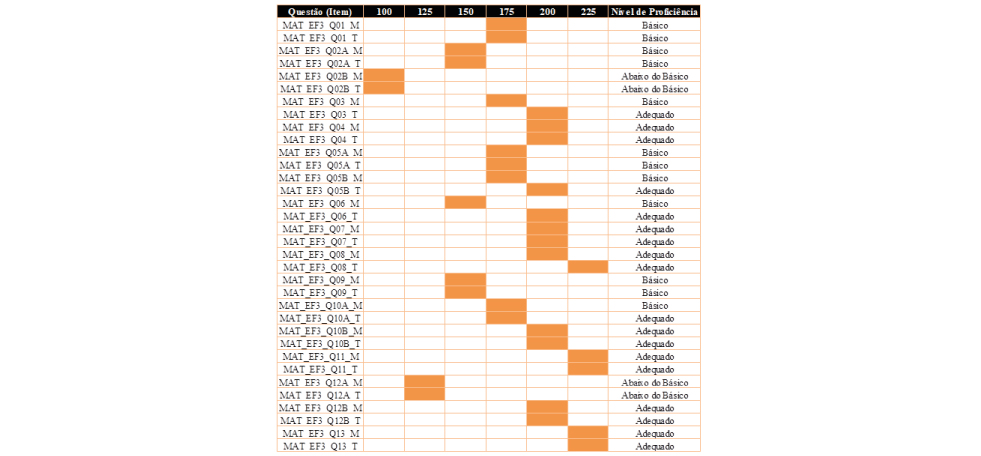
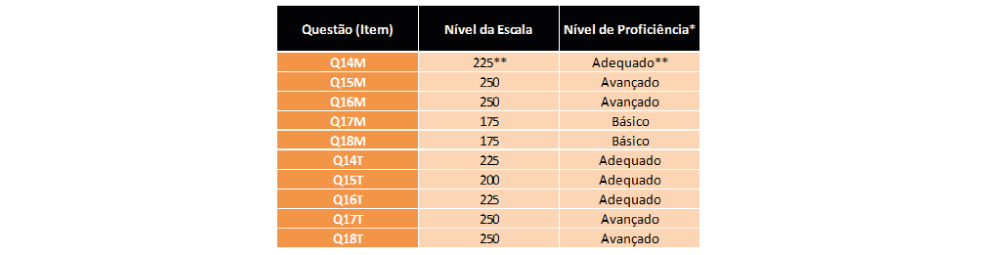
Tabela 2 – Posicionamento e Classificação dos Itens de Múltipla Escolha na Escala de Matemática do SARESP - 3º Ano do Ensino Fundamental
3. ANÁLISE DO DESEMPENHO DOS ALUNOS DO 3º ANO DO ENSINO FUNDAMENTAL POR HABILIDADE AVALIADA EM MATEMÁTICA
A seguir, serão apresentadas as tarefas propostas para as 13 questões de resposta construída da edição 2019 da prova SARESP para o 3º ano do Ensino Fundamental. A apresentação foi organizada agrupando os itens que tratam os mesmos conteúdos:
Números e Operações: questões 1, 2, 3, 5, 7 e 13.
Espaço e Forma: questões 6 e 8.
Grandezas e Medidas: questões 4 e 10.
Tratamento da Informação: questões 9, 11 e 12.
Serão apresentados os enunciados das questões, tanto da prova da manhã (coloração azul), como da prova da tarde (coloração laranja) para cada item proposto e a solução esperada.
3.1. ITENS SOBRE NÚMEROS E OPERAÇÕES
Em relação ao tema Números e Operações, as análises das questões e do desempenho dos alunos serão divididas em dois grupos: Sistema de Numeração Decimal e Operações.
3.1.1. Sistema de Numeração Decimal
Os itens que abordaram essa temática foram as da abertura da prova, ou seja, as questões 1, 2A e 2B. Tais questões tinham como objetivo avaliar a habilidade dos estudantes para produzir escritas numéricas, além de estabelecer comparações entre números naturais, possibilitando apreender se os estudantes compreendem algumas noções do funcionamento do Sistema de Numeração Decimal.
3º ANO - Questão 1: Avaliar a produção de escrita numéricas, a partir de um ditado, demonstrando compreender as regras do Sistema de Numeração Decimal.

Os números para o ditado do período da manhã foram: 27, 91, 330, 843 e 2011, enquanto para a prova da tarde, foram: 32, 84, 220, 941, 2011.
Assim, cabia ao aluno fazer o registro dos números ditados, sendo dois da ordem de dezena, dois da ordem de centena e um da ordem de unidade de milhar. O intuito era perceber como os alunos chegaram ao 3º ano produzindo a escrita numérica, atentando-se para o valor posicional dos algarismos.
A tarefa de escrever os cinco números ditados foi concluída corretamente pela maioria dos estudantes (em torno de 75%) e, se considerarmos aqueles que escreveram pelo menos quatro números corretamente, o índice de acerto se aproxima de 90%.
Trata-se de um bom índice – tais resultados sugerem que a escrita numérica é bem assimilada pelos alunos ao final do 3º Ano do Ensino Fundamental.

No exemplo acima, é possível observar que o aluno registrou adequadamente os números da ordem de dezena e também de unidade de milhar (provavelmente por se tratar de um número similar a um presente em seu cotidiano – o ano). Mas nos dois números da ordem de centena, provavelmente, por ainda não possuir muita familiaridade, a criança ao realizar o seu registro, altera os valores ditados devido ao erro de posicionamento dos algarismos.
É provável que esse aluno compreenda razoavelmente a escrita numérica, principalmente de números presentes em seu dia a dia, mas precisa avançar na compreensão da escrita numérica, principalmente da ordem de centena – uma possibilidade de trabalho para auxiliar no avanço dessa escrita é o uso de fichas sobrepostas para a composição numérica.
A utilização de diferentes materiais e formas de registros é fundamental para ampliar as ideias das crianças a respeito dos números, auxiliando na compreensão do SND, principalmente no uso do algarismo zero nas diferentes ordens. Outra possibilidade para auxiliar no avanço dessa habilidade é o uso do ábaco associado a grafia dos números, levando os alunos a compreenderem, principalmente o uso do zero em ordens “vazias”:

3º ANO - Questões 2A e 2B: Avaliar a habilidade de comparar escritas numéricas de diferentes ordens, identificando o maior e o menor número.

Para estas questões foram apresentados cinco números aos alunos. A partir desses números, para resolver corretamente a questão 2A, o aluno deveria compara-los e determinar o maior dentre eles, e para solucionar a questão 2B, deveria identificar o menor. Para tanto, uma possibilidade inicial seria analisar a quantidade de algarismos que os números apresentados possuíam, sendo que os números com maior quantidade de algarismo são sempre maiores do que aqueles escritos com uma quantidade menor de algarismos.
Assim, para a questão 2A, utilizando essa estratégia, o aluno poderia eliminar 3 números e ficar entre 1997 e 3100, no caso da prova da manhã, e entre 1878 e 3200, no caso da prova da tarde. Esses números foram intencionalmente escolhidos na elaboração dos itens, com o intuito de perceber se os alunos estabelecem as relações necessárias a partir da casa de maior valor posicional, ou seja, o primeiro algarismo da esquerda para direita. Nesse caso, a análise da criança deve ser que o número 1000 é menor que 3000, e não que o 7 é maior que 0, caso faça a comparação a partir das unidades. Cerca de 90% dos estudantes conseguiram identificar corretamente o maior número e apenas 6% escolheram o outro número com quatro algarismos.
Para a questão 2B, bastaria que o aluno fizesse a primeira comparação (entre quantidade de algarismos dos números), uma vez que apenas um número apresentado possuía dois algarismos. Neste caso, o número de acertos foi próximo de 97%, revelando um bom desempenho.
Assim, é perceptível que a maioria dos alunos possui essa habilidade bem desenvolvida, considerando-se números de até a ordem de unidade de milhar.
3.1.2. Operações
As questões envolvendo operações são as de número 3, 5A, 5B, 7 e 13. Todas essas questões apresentavam situações-problema, exigindo do aluno a interpretação de qual cálculo seria necessário para a resolução, exceto a de número 7, que envolvia a resolução de uma conta de subtração, sem contextualização.
3º ANO - Questão 3: Avaliar a habilidade de resolver uma situação-problema do campo multiplicativo (soma de parcelas iguais)

Na questão de número 3 da prova do 3º ano foi apresentada aos alunos uma situação-problema do campo multiplicativo. Nas propostas da manhã e da tarde, os estudantes deveriam interpretar a situação e resolve-la utilizando a estratégia que melhor lhe conviessem: multiplicar 5x6, fazer adições sucessivas, cálculo mental, desenhar a situação, de maneira que chegassem ao resultado 30.

Aproximadamente 80% dos alunos chegaram a resposta correta. Vale destacar que cerca de 7% dos alunos somaram os números presentes no enunciado, ou seja, fizeram 5 + 6 = 11, demonstrando não compreenderem a situação proposta ao somarem número de bandejas e quantidade de produtos em cada bandeja.

Apesar de ser um número relativamente pequeno perto do percentual de acertos, esse dado merece atenção e reflexão de como as diferentes operações, situações-problema e estratégias de resolução são trabalhadas em sala de aula. É comum, diante de uma situação-problema, o aluno apenas coletar do enunciado os números presentes e realizar uma operação, sem compreender o que se espera.
Refletir na ênfase que é dado no trabalho em sala de aula ao cálculo, principalmente no uso dos algoritmos convencionais, faz-se necessário, pois muitas vezes é realizado em detrimento da compreensão da situação proposta, ou mesmo, apresentado como única possibilidade correta de resolução, levando os alunos a entenderem situações-problema como “pretextos” para averiguação de cálculos e não situações contextualizadas que podem ser resolvidas através de diversas estratégias.
É importante propiciar a discussão de diversas situações-problema, com diferentes propósitos, além de validar as distintas estratégias das crianças, ao permitir que socializem com os colegas a maneira como pensaram para chegar a resposta, ampliando assim o repertório de toda turma, trazendo benefícios a aprendizagem de todos.
3 º Ano - Questão 5A e 5B: Avaliar a habilidade de decompor um número em duas parcelas

A questão de número 5A para envolveu a descoberta de dois números cuja a soma resultasse no valor proposto (74 para prova da manhã e 56 para prova da tarde). Havia diferentes possibilidades de resposta para esse item e cerca de 85% dos alunos obtiveram êxito nesse item. Esse tipo de proposta é uma possibilidade de introdução ao pensamento algébrico, campo da Matemática que vem ganhando espaço nos Anos Iniciais recentemente.
Cerca de 14% dos alunos não conseguiram executar essa atividade, optando por números cuja soma não totalizavam o resultado indicado, nem se aproximavam (um a mais ou um menos), indicando a necessidade de um olhar do professor sobre as possibilidades de trabalho com propostas de cálculos menos diretivos (cálculos dados), estimativa, decomposição numérica (essencial ao cálculo mental), entre outros.
A maioria dos alunos que acertaram, optaram por um número múltiplo de 10 na primeira parcela e a partir desse número pensaram no quanto faltava para a resposta. Também foi perceptível que muitos alunos tentaram encontrar duas parcelas iguais, apesar de não ser um pré-requisito da situação proposta neste ano, mas uma estratégia válida.

O item 5B da prova do 3º ano era de resposta única e o aluno deveria descobrir o número que completaria a operação de maneira que ficasse correta. Uma possibilidade seria o estudante fazer o cálculo do primeiro número apresentado menos o resultado (45-11=34), ou então pensar quanto do número inicial precisaria ser retirado para chegar ao resultado.
O índice de acerto desse item foi um pouco menor que o item A dessa mesma questão, cerca de 75%. Apesar de alto o índice de acerto, aproximadamente 20% dos respondentes não chegaram próximos ao resultado (um a mais ou um a menos), indicando que esse tipo de situação merece atenção em sala de aula.
3º ANO - Questão 7: Avaliar a capacidade de calcular o resultado de uma subtração, com recurso.

Nesse item o aluno deveria calcular uma subtração com recurso. A maneira mais usual observada nas soluções dos estudantes foi o uso do algoritmo.

O percentual de acerto foi de aproximadamente 65%, um índice relativamente baixo se comparado às outras questões envolvendo operações, porém apresentadas na forma de situações-problema. O número de alunos que fez a adição em vez da subtração foi irrisório (0,3%).
Aproximadamente 6% dos alunos errou ao subtrair o menor do maior algarismo de mesma ordem, como no exemplo a seguir.
3º ANO - Exemplo de resposta encontrada:

A maior concentração de erros (quase 28%) se deu por outros motivos que não aqueles esperados e utilizados na elaboração dos critérios de correção, merecendo investigação mais aprofundada.
3º ANO - Questão 13: Avaliar a resolução de situação-problema envolvendo duas operações do campo aditivo.

Para resolver essa situação-problema, o aluno deveria descobrir a quantidade de um determinado sabor (brigadeiro para a prova da manhã e sorvete para a prova da tarde) que foi vendido, a partir da informação do total dos tipos de produtos vendidos nesse dia e da quantidade de outros dois sabores embutidos nas vendas.
Uma possibilidade de resolução seria adicionar a quantidade dos dois sabores conhecidos e, então, subtrair do total vendido. Outra possibilidade seria realizar duas subtrações: subtrair a quantidade de um dos sabores do total e, em seguida, subtrair a quantidade do outro sabor do resultado obtido anteriormente.
Baseado no percentual de acerto, pode-se considerar que esse é um dos itens mais difíceis da prova – cerca de 52% dos alunos acertaram o item, ficando acima apenas do índice de acerto da questão 11, de leitura de tabela. Aproximadamente 4% dos alunos erraram por um a mais ou um a menos e outros 4% somaram os números apresentados no enunciado, demonstrando não compreenderem a situação apresentada.
Os erros se concentraram em sua maioria no critério de correção “outras respostas”, uma possibilidade é que os alunos tenham se perdido durante a resolução, uma vez que precisavam fazer dois cálculos, indicando que este tipo de situação precisa ser trabalhada com maior frequência e atenção em sala de aula.
3º ANO - Exemplo de resposta encontrada:

Nesse exemplo, é possível perceber a estratégia do aluno: ele soma os dois sabores fornecidos (18 + 13 = 31) e, provavelmente, por tentativa e erro, testou possibilidades de quantidades que completariam o 31 até o 37. Na primeira tentativa, indicou o 5 e chegou ao resultado de 36. Percebendo que não havia chegado na resposta correta, refaz todo o cálculo e dessa vez opta pelo número 6 e averigua que essa era a quantidade correta. Fica claro que o aluno compreendeu a situação proposta e usa de suas estratégias pessoais para chegar ao resultado.
3º ANO - Exemplo de resposta encontrada:

Nesse outro exemplo, a estratégia utilizada pela criança foi desenhar os brigadeiros dos diferentes tipos. Provavelmente, a criança desenhou os brigadeiros informados e por fim, desenhou os de maracujá até completar os 37 brigadeiros, também demonstrando compreender bem a situação proposta e boa organização para resolução.
3.2. ITENS ENVOLVENDO ESPAÇO E FORMA
No ano de 2019, a prova do SARESP trouxe mais um item para avaliar os conteúdos de Espaço e Forma. Duas questões compõem essa temática na prova do 3º ano: o item 6 e o item 8, que analisaremos a seguir.
3.2.1. Forma
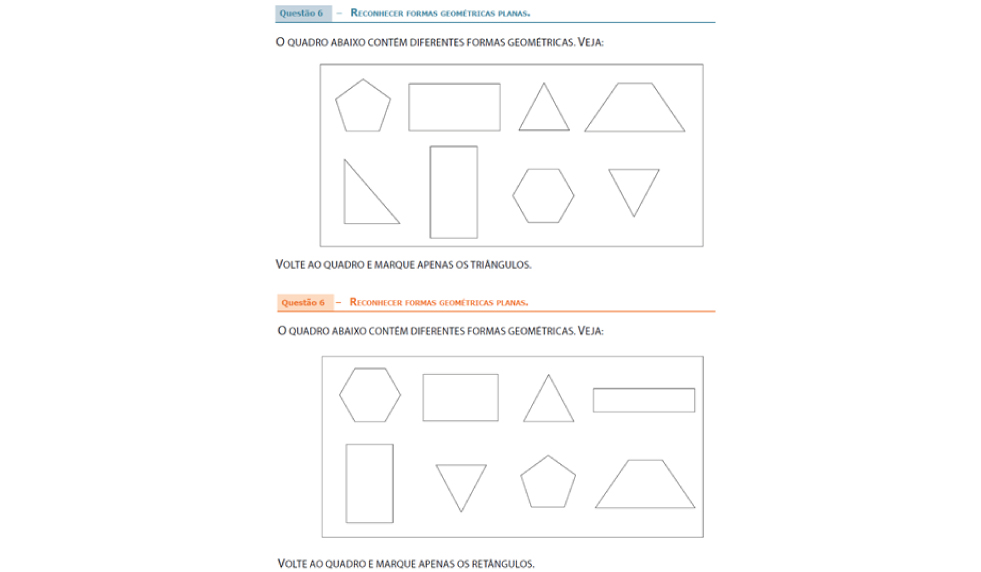
Na questão 6 foram apresentadas oito figuras planas aos alunos e estes, na prova da manhã, deveriam reconhecer quais dentre essas eram triângulos, e na prova da tarde, quais eram retângulos.
Nesta questão houve discrepância entre os resultados da manhã e da tarde. Sendo assim, pode-se concluir que reconhecer retângulos é mais desafiador do que reconhecer triângulos para os alunos do 3º ano.
Na prova da manhã, quase 87% dos alunos identificaram os três triângulos corretamente. Outros 9,4% dos alunos identificaram um ou dois triângulos corretamente. Pode-se observar, que a maioria dos alunos que identificaram dois triângulos, deixaram de marcar o triângulo retângulo – isso mostra uma tendência de se apresentar, geralmente, nos Anos Iniciais triângulos na representação equilátera, o que necessita ser repensado, pois acaba engessando a forma da criança conceber um triângulo.
3º ANO - Exemplo de resposta encontrada:

Na prova da tarde, quase 70% dos alunos indicaram os três retângulos do item. Indicaram um ou dois retângulos cerca de 14% dos respondentes. Vale destacar que aproximadamente 10% dos alunos indicaram formas não retangulares, que se deve principalmente pela confusão que as crianças fazem entre as nomenclaturas retângulo e triângulo, indicando mais um ponto que necessita de atenção no trabalho pedagógico. Também muitas crianças indicaram o pentágono e o hexágono, demonstrando não possuírem familiaridade com as figuras planas.
3.2.1.
Localização Espacial
3º ANO - Questão 8: Avaliar a habilidade de identificar a movimentação e a localização final de um objeto, indicando compreensão do significado de “vire à direita” ou “vire à esquerda”.

A questão de número 8 da prova avaliou se o aluno identifica a movimentação de um caminhão em um estacionamento, revelando compreender os comandos “vire à direita” e “vire à esquerda”, respondendo corretamente em qual vaga o caminhão estacionará.
3º ANO - Exemplo de resposta encontrada:

Aproximadamente 65% dos alunos responderam corretamente, indicando compreenderem as instruções do comando do item. Cerca de 10% dos alunos inverteu direita/esquerda em apenas um dos movimentos, provavelmente no segundo comando, demonstrando dificuldades quando o ponto de referência muda em relação a posição inicial. Outros 10% indicaram a vaga 2 ou 3, errando provavelmente por não se atentarem que o caminhão deveria entrar na segunda entrada e não na primeira.
A aprendizagem envolvendo deslocamento no espaço é desafiadora aos alunos. Para essa aprendizagem, deve-se partir de propostas de trabalho em que as crianças de fato se desloquem por diferentes espaços, apreendendo as direções a partir do próprio corpo. Porém, é fundamental auxiliar os alunos a transporem esse conhecimento para o papel, através de diversas formas de registros (desenho, uso de malha quadriculada, mapa de sala, etc.).
3.3.
ITENS ENVOLVENDO MEDIDAS
3.3.1.
Situação-problema envolvendo medida de massa
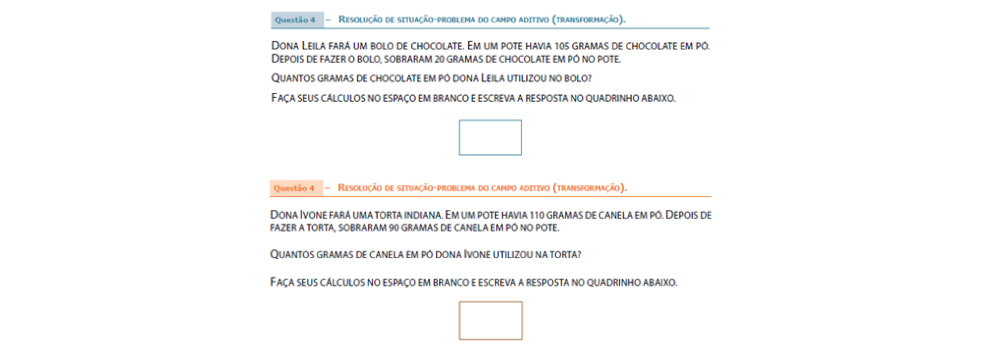
Na questão 4 foi proposta uma situação-problema na qual uma pessoa está fazendo uma receita e são informadas as quantidades de um determinado ingrediente antes da realização da receita e após o seu término. O aluno poderia realizar uma subtração e descobrir quantos gramas desse ingrediente foram utilizados na receita.
No período da manhã cerca de 65% dos alunos chegaram ao resultado correto e no período da tarde, quase 70% dos alunos. Os cálculos propostos para os dois períodos envolviam o uso do recurso na ordem da dezena.
3º ANO - Exemplo de respostas encontradas:

Foi possível observar que muitas crianças optaram pelo uso do algoritmo para a resolução. Cerca de 8% no período da manhã e 4% no período da tarde erraram, pois subtraíram o maior algarismo do menor, em vez de fazer o empréstimo necessário para a dezena.
Vale destacar nesse item, que a contagem de quanto faltava para chegar de um número ao outro (90 para 110, principalmente) seria muito mais simples do que realização do algoritmo da subtração. Por exemplo, no período da tarde, o aluno deveria fazer o cálculo 110 – 90 = 20. Ao realizar o algoritmo da subtração, a criança necessitaria fazer o empréstimo para a dezena, ao passo que, se pensasse quanto faltava do 90 para o 110, contando de 10 em 10, chegaria rapidamente ao resultado, sem grandes dificuldades. O que se deseja apontar com isso, é a necessidade de se trabalhar com as crianças diferentes formas de resolução, valorizando diferentes estratégias, de maneira que percebam, de acordo com a proposta, com qual forma de resolução se sentem mais seguras ou mesmo, alcançam o resultado mais rapidamente.
Cerca de 21% dos alunos na prova da manhã e 26% na da tarde apresentaram respostas diferentes das detalhadas nos critérios de correção e, portanto, foram categorizadas como “outras respostas”.
3.3.2. Itens sobre valores de células e moedas
3º ANO - Questão 10A e 10B: Avaliar a habilidade calcular o valor total de uma certa quantia de cédulas e moedas, assim como o valor dividido igualmente em dois.

A questão 10 possuía duas tarefas: uma com o intuito de avaliar o reconhecimento do valor de cédulas e moedas apresentadas para determinar o valor total de uma quantia (10A) pelos alunos, e a outra, se eles conseguem dividir o valor apresentado em duas partes iguais (10B).
3º ANO - Exemplo de resposta encontrada:

O total de alunos que acertaram o item 10A foi em torno de 85%, tanto no período da manhã, como no da tarde, indicando bom reconhecimento do valor de cédulas e moedas do nosso sistema monetário.
Já o item 10B mostrou-se mais desafiador aos alunos do que o item 10A, pois cerca de 66% dos respondentes acertaram. O aluno que errou a questão 10A, provavelmente também errou o item 10B, uma vez que se deveria dividir o valor total (item 10A) em duas partes iguais.
3º ANO - Exemplo de resposta encontrada:

Assim como apontado em outros itens, a resolução predominante para o cálculo do item 10B foi o algoritmo convencional.
3.4. ITENS ENVOLVENDO TRATAMENTO DA INFORMAÇÃO
Para avaliar as habilidades dos alunos de noções relativas ao bloco de conteúdos Tratamento da Informação foram propostas as questões 9, 11 e 12, que envolvem a leitura de calendário, gráfico e tabela.
3º ANO - Questão 9: Avaliar a habilidade de ler informações contidas no calendário.

A tarefa proposta nessa questão envolvia a identificação da data de um aniversário a partir da localização no calendário da primeira segunda-feira do mês apresentado.
3º ANO - Exemplo de resposta encontrada:

Os alunos mostraram bom desempenho nesse item, em torno de 87% dos alunos responderam corretamente, indicando que a leitura de calendário é trabalhada de maneira adequada e consistente na rede paulista.
3º ANO - Questão 11: Avaliar a habilidade de ler dados expressos em tabelas e identificar dados nela apresentados.
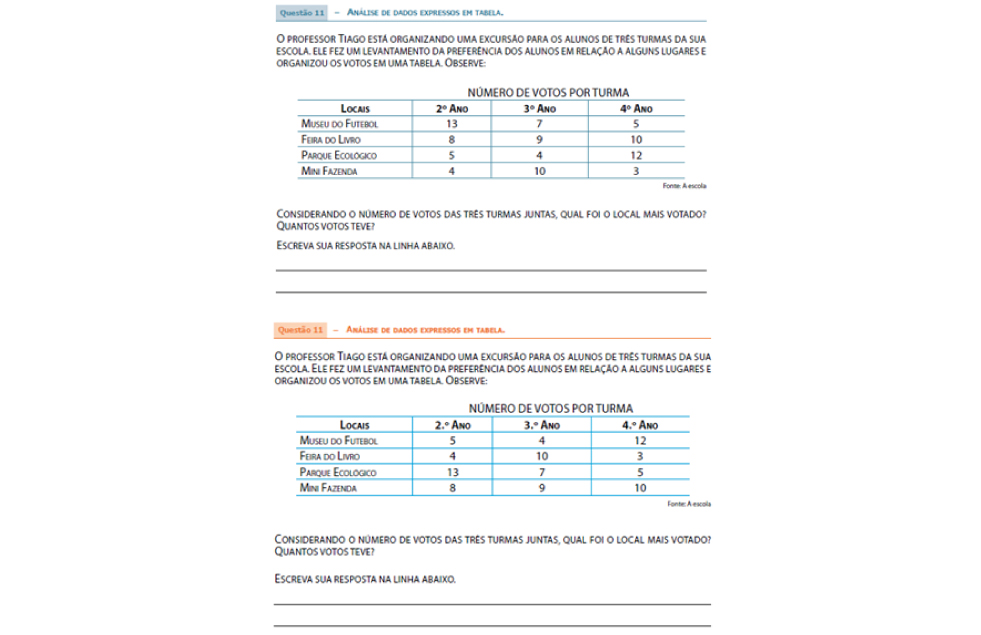
O problema proposto nesse item envolvia a análise da tabela para identificação do local mais votado para uma excursão, levando-se em consideração os votos de três turmas. Para tanto, o aluno deveria calcular o total de votos de cada opção de passeio e compará-los, no intuito de definir o mais votado.
3º ANO - Exemplo de resposta encontrada:

A criança do exemplo acima, compreendeu a situação proposta, realizou a leitura correta da tabela, somando as três colunas. Dentre os valores obtidos, identificou o maior e escreveu as duas respostas esperadas (local e total de votos).
Vale destacar que a resposta não estava atrelada ao maior valor explícito na tabela – cerca de 6% dos alunos indicaram essa resposta, quantidade relativamente baixa, mas que revela a dificuldade de parte das crianças em interpretar o problema e a tabela, como no exemplo a seguir:
3º ANO - Exemplo de resposta encontrada:
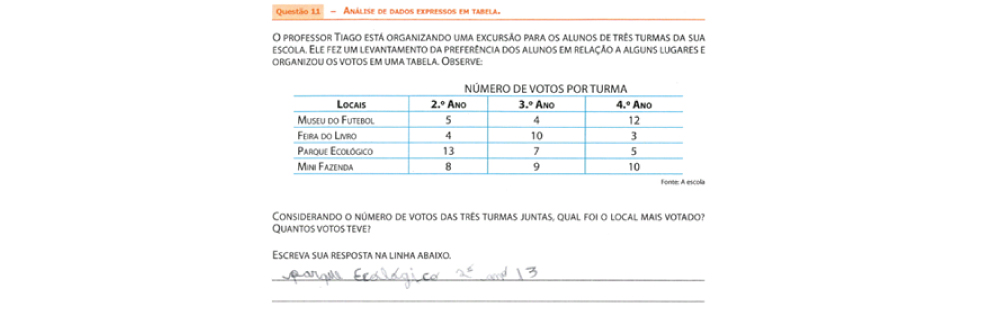
O percentual de acerto dessa questão em relação a questão de mesma habilidade da edição de 2018 teve uma redução significativa – em torno de 48% dos alunos responderam corretamente, enquanto que na edição passada cerca de 90% acertaram.
Uma possibilidade dessa redução é que o item, para ser considerado correto, exigia duas informações: a indicação do local e o número de votos totais desse. Porém, ao somarmos os alunos que acertaram local e número de votos com os alunos que indicaram ou apenas o local correto, ou apenas o número total de votos apenas, temos 63% de acerto, número ainda inferior ao resultado de 2018.
3º ANO - Questão 12A e 12B: Avaliar a habilidade de realizar a leitura de gráficos de barra simples e resolver situação envolvendo a comparação de dados expressos em gráficos.

A questão de número 12 propôs duas tarefas: uma envolvia a identificação do número de votos de determinado animal estudado (item 12A), e a outra analisou a habilidade de comparar duas informações expressas no gráfico para apontar quantos votos uma teve a mais que a outra (item 12B).
Para a prova desse ano, optou-se por um gráfico de barras em vez de um gráfico de colunas, como foi proposto em outras edições da prova SARESP.
O aluno, para a solução de ambos os itens, necessitava ler corretamente o gráfico, no intuito de identificar o número de votos que cada entrada obteve, sendo necessário atentar-se para o fato do gráfico apresentar variação de 2 em 2 unidades para cada marcação no eixo horizontal.
3º ANO - Exemplo de resposta encontrada:

O índice de acerto foi superior a 93% no item 12A, indicando que os alunos possuem familiaridade com esse tipo de gráfico e facilidade para leitura de dados evidentes. Já no item 12B o índice de acerto girou em torno de 73%, indicando que os alunos apresentam maiores dificuldades quando, além de interpretar os dados, necessitam relaciona-los, mesmo que seja um cálculo simples (10 – 8 = 10).
3.5. ÍNDICE DE DIFICULDADE DA PROVA SARESP 2019
A partir da apresentação dos resultados obtidos pelos estudantes do 3º ano do Ensino Fundamental na edição 2019 da prova SARESP, as questões foram classificadas de acordo com o grau de dificuldade aferido.
3.5.1. Índice de dificuldade da prova do 3º ano EF – SARESP 2019
As figuras a seguir ilustram a distribuição dos itens segundo a classificação da Teoria Clássica dos Testes (TCT).
Figura 1.1 – Classificação das questões da prova SARESP – 3º Ano EF 2019, período da manhã, segundo grau de dificuldade percebido pelos respondentes.

Obs.: Os intervalos considerados são fechados somente à esquerda e, portanto, os percentuais das questões são maiores ou iguais que os valores da esquerda e estritamente menores que os valores da direita do intervalo.
Figura 1.2 – Classificação das questões da prova SARESP – 3º Ano EF 2019, período da tarde, segundo grau de dificuldade percebido pelos respondentes.
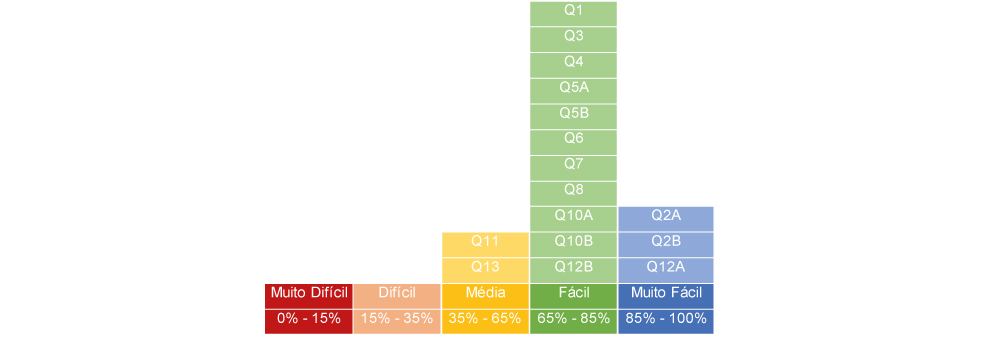
Obs.: Os intervalos considerados são fechados somente à esquerda e, portanto, os percentuais das questões são maiores ou iguais que os valores da esquerda e estritamente menores que os valores da direita do intervalo.
As figuras a seguir ilustram as questões que foram respondidas corretamente por, no mínimo, três quartos (75%) dos alunos.
Figura 2.1 – Distribuição das questões segundo percentual de acerto – SARESP 2019 – 3º Ano EF, período da manhã

Obs.: Os intervalos considerados são fechados somente à esquerda e, portanto, os percentuais das questões são maiores ou iguais que os valores da esquerda e estritamente menores que os valores da direita do intervalo.
Figura 2.2 – Distribuição das questões segundo percentual de acerto – SARESP 2019 – 3º Ano EF, período da tarde

Obs.: Os intervalos considerados são fechados somente à esquerda e, portanto, os percentuais das questões são maiores ou iguais que os valores da esquerda e estritamente menores que os valores da direita do intervalo.
Frente a essa distribuição, cabe ressaltar sobre a prova do 3º ano que
- A prova se mostrou fácil para a maioria dos alunos, havendo uma concentração de questões classificadas como fáceis e muito fáceis.
- Os alunos apresentaram índice de acerto superior a 75% no período da manhã em 9 questões e no período da tarde em 7 questões, o que sugere um domínio de tais tarefas por parte significativa dos estudantes.
- Apenas uma questão teve índice de acerto inferior a 50%, merecendo destaque dentre os conteúdos explorados.
A análise dos resultados sugere que a investigação das questões envolvendo as habilidades que foram respondidas corretamente por, no mínimo 75% dos alunos, se propostas novamente nas próximas edições da prova de Matemática no SARESP precisam ser repensadas, de modo a investigar e aferir se os alunos conseguem responder questões ainda mais desafiadoras, dado o bom desempenho em seguidas edições.
4. CONSIDERAÇÕES FINAIS – MATEMÁTICA NO 3º ANO DO ENSINO FUNDAMENTAL
Na edição de 2019, a média da rede estadual paulista na prova do 3º ano foi igual a 212,9, sendo classificada no nível Adequado, de acordo com os intervalos de proficiência adotados no SARESP. Isso significa que os alunos nesse nível de escolaridade estão demonstrando domínio da maioria das expectativas de ensinos atreladas às habilidades que compõem a avaliação. Desse modo, é esperado que a maioria dos alunos se mostre capaz de resolver as tarefas ancoradas em níveis inferiores à média, independentemente da edição da prova. Com isso, é possível detalhar uma coletânea de tarefas que se espera que esses alunos sejam capazes de realizar se considerarmos desde a edição 2014, quando se passou a utilizar a TRI na análise das provas dessa turma. Por outro lado, o desafio a ser superado por esses estudantes passa a ser as tarefas que ancoram nos níveis 225, ponto de ancoragem subsequente a média da turma.
O bom resultado dessa edição é reforçado pelo baixo percentual de estudantes que apresentaram proficiência classificada como Abaixo do Básico. Esses alunos, precisam de atenção especial em sala de aula e através de ações educativas terem suas necessidades atendidas para que possam desenvolver melhor as habilidades matemáticas necessárias para esse início de escolarização. A partir dos resultados obtidos, pode-se aferir que para o 3º ano
- A atividade que envolveu leitura de tabela e identificação de dados nela apresentados mostrou-se a mais desafiadora da prova, com índice de acerto abaixo dos 50%, indicando a necessidade de fortalecimento dessa habilidade;
- Dentre as situações-problema propostas, a que os alunos apresentaram maior dificuldade foi a envolvendo a ideia de descobrir a quantidade de um tipo de produto, dado a quantidade de outros dois tipos e a quantidade total desses três tipos juntos, que envolvia dois cálculos, sugerindo que esse tipo de situação é pouco trabalhado com os alunos;
- Dentre os cálculos necessários para a realização da prova, o que os alunos mais encontram dificuldades foi no cálculo da subtração com recurso, no qual não havia uma situação-problema envolvida;
- A questão que envolvia comparação de números foi a que os alunos tiveram mais facilidade;
- Apesar do bom desempenho dos alunos na questão de identificação de figuras planas, a diferença entre resultado das provas da manhã e da tarde indica que esse assunto precisa ser mais explorado para obtenção de mais dados;
- Os alunos apresentam bom domínio da habilidade de leitura de calendário, indicando a necessidade de outras formas de exploração desse item em provas futuras;
- O item para localizar a posição de um objeto mediante informações dadas mostrou-se mais desafiador do que edições anteriores;
- A mudança do tipo de gráfico apresentado foi positiva, possibilitando identificar que os alunos também possuem boa proficiência em gráficos de barras. O desempenho consistente dos alunos revela que eles podem ser expostos a novas situações, inclusive problemas mais desafiadores ou de temáticas mais variadas, sendo possível assim aferir com melhor precisão as mais diversas habilidades dos alunos
.
Os alunos cuja proficiência situa-se no nível Avançado encontram poucas tarefas características do seu nível de proficiência apenas nos itens de múltipla escolha, o que significa dizer que é preciso explorar as questões discursivas de modo a propor novas situações que melhor diferencie os alunos do nível Adequado dos níveis anteriores.
As questões envolvendo números e operações têm sido bem exploradas nas edições do SARESP e diante do bom desempenho dos alunos do 3º ano nesses conteúdos, é importante buscar o equilíbrio com as outras áreas da Matemática, tão importantes quanto essa. Nesta edição, tivemos uma questão relacionada a grandezas e medidas nos itens de resposta construída, além de modificações no tipo de gráfico apresentado e introdução de mais um item relacionado a espaço e forma, possibilitando a obtenção de novos dados para análise. Com a implementação da Base Nacional Comum Curricular, essas e outras áreas, como o pensamento algébrico e a probabilidade, precisam ganhar espaço na avaliação, de maneira a trazer dados a comunidade educacional, auxiliando no trabalho desenvolvido com as crianças.
A análise do desempenho dos alunos do 3º ano do Ensino Fundamental é uma possibilidade rica para se repensar o que precisa ser fortalecido no ensino, no intuito que os alunos avancem cada vez mais em suas aprendizagens. |
 |
|
|
|

|
