|
|
 |
A edição 2019 do SARESP aferiu a proficiência dos estudantes da 3ª série do Ensino Médio, sendo que a média obtida foi igual a 276,6. Esse valor indica um nível de proficiência classificado como Básico para a turma em questão. Importante ressaltar a percepção de pequena oscilação para baixo na média de proficiência da turma, demonstrando que o Ensino Médio ainda representa um grande desafio para obtenção de avanços consistentes como aqueles observados nas turmas avaliadas no Ensino Fundamental. Destaca-se também a redução do percentual de alunos do nível Básico e aumento tanto para o nível Abaixo do Básico como para o Adequado e Avançado.
A seguir, são apresentados exemplos comentados a fim de ilustrar atividades características que os alunos foram capazes de realizar ou que demonstraram dificuldades. Além do enunciado e da solução dos itens, há a indicação de alternativas de trabalho, além de uma representação gráfica da frequência de escolha de cada alternativa nos três Grupos de Desempenho e a Curva Característica do Item que associa a proficiência do respondente e a probabilidade de acertar a questão.
Exemplo 1
Nível Básico
Compõe a descrição do ponto 300 da Escala de Matemática – SARESP

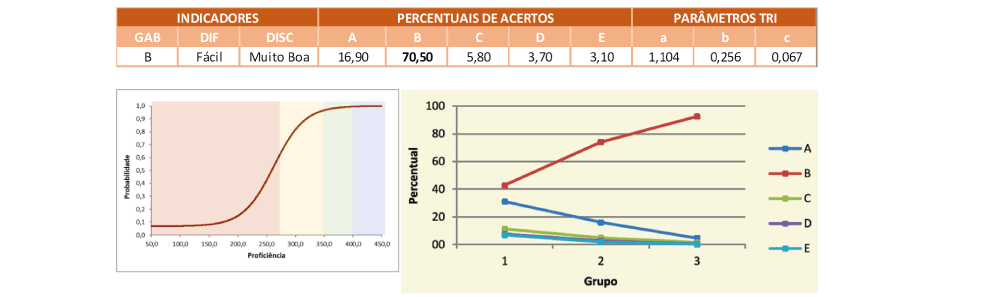
O item está atrelado a habilidade H02 – Resolver problemas que envolvam progressões aritméticas – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o assunto é tratado logo no 1º bimestre da 1ª Série do Ensino Médio. A tarefa proposta no item envolve a determinação do número de exercícios realizados por um estudante determinado dia, dado a quantidade de exercícios feita no 1º dia e que ele sempre faz 2 exercícios a mais do que no dia anterior, caracterizando assim uma Progressão Aritmética (PA).
Nesse caso, a solução pode ser obtida de diferentes maneiras, inclusive o detalhamento dia a dia do número de exercícios resolvidos. Veja:

Esse método, apesar de válido, nem sempre é funcional, a depender da situação investigada. Cabe ao professorado atentar-se para tanto e mostrar para seus alunos a importância de não depender exclusivamente desse método.
O uso do termo geral de uma PA também é uma opção para obtenção da resposta. Observe:

Outra opção para obtenção da alternativa correta seria observar que do dia inicial até o 15º dia se passaram 14 dias. Como para cada dia tem-se como meta aumentar 2 exercícios, então após os 14 dias haverá um aumento de 28 exercícios em relação ao 1º dia, ou seja, no 15º dia serão feitos 28 exercícios a mais do que os 3 exercícios feitos inicialmente, ou seja, no 15º dia serão feitos 31 exercícios (alternativa B).
O item foi respondido corretamente por aproximadamente 70% dos alunos, o que faz com que a tarefa seja classificada como fácil, sendo que o índice de acerto foi de 42,9% no Grupo de Menor Desempenho, 74,1% no Grupo Intermediário e de 92,5% no Grupo de Maior Desempenho, o que refletiu em um item cuja discriminação foi considerada muito boa entre os Grupos.
Segundo a Curva Característica do Item, os alunos cuja proficiência é próxima da média da rede estadual tem probabilidade de acerto variando entre 60% e 70%, o que reforça a expectativa de que a maioria dos respondentes são capazes de mobilizar conhecimentos para resolver essa tarefa.
Ao analisar a distribuição das respostas nos Grupos de Desempenho observa-se que a alternativa correta foi a alternativa com maior percentual de escolha em todos os Grupos, enquanto que a alternativa (A) foi a segunda mais atrativa, possivelmente sendo escolhida por aqueles que fizeram termo a termo e pularam valores ou então que utilizaram a fórmula do termo geral de forma incorreta, por exemplo utilizando  ao invés da expressão correta ao invés da expressão correta 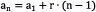 . Além disso, as alternativas (C), (D) e (E), juntas, atraíram pouco mais de 12% dos candidatos, apesar de os valores presentes nessas alternativas serem inferiores a 28, o que sugere uma incompreensão ou a não análise frente ao resultado obtido como resolução do problema. . Além disso, as alternativas (C), (D) e (E), juntas, atraíram pouco mais de 12% dos candidatos, apesar de os valores presentes nessas alternativas serem inferiores a 28, o que sugere uma incompreensão ou a não análise frente ao resultado obtido como resolução do problema.
Vale destacar que os números 29 e 33 não foram propostos como distratores, mas podem ser postos para análise em sala de aula. Esses números são os termos anterior e seguinte de , sendo uma opção de resposta plausível, principalmente para quem faz uso da opção termo a termo. Também é recomendado ao professorado explorar variações desse tipo de problema, seja no cenário ou na pergunta. Um equívoco comum observado é a não percepção da diferença entre a pergunta proposta no problema (o número de exercícios resolvidos no 15º dia de estudo) e outra, bem próxima, que remete a soma dos termos da PA, que seria: qual o número de exercícios resolvidos ao longo de 15 dias de estudos? |
 |
Exemplo 2
Nível Básico
Compõe a descrição do ponto 300 da Escala de Matemática – SARESP
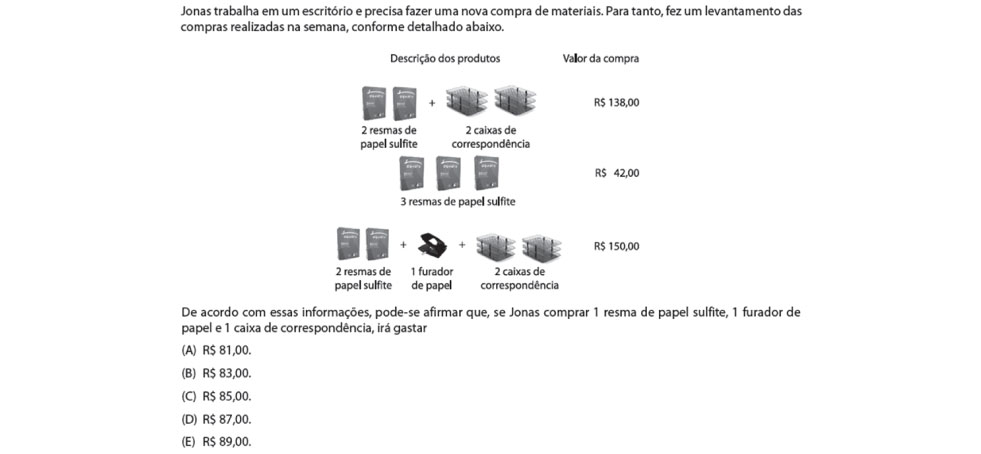

O item está atrelado a habilidade H14 – Resolver situações-problema por intermédio de sistemas lineares até a 3ª ordem – segundo a Matriz de Referência de Avaliação do SARESP, sendo que sistemas lineares é um assunto tratado no 2º bimestre da 2ª Série do Ensino Médio. A tarefa proposta envolve a determinação do preço da compra de um item de cada produto apresentado no problema, tendo como base três compras anteriores envolvendo esses itens.
A solução pode ser obtida de diferentes maneiras, sendo que no problema proposto não é necessário o uso de modelagem via sistema ou mesmo técnicas para resolução de um sistema linear, uma vez que o esquema apresentado se trata de um sistema já escalonado.
Mediante isso, uma maneira de obter a solução do problema envolve os seguintes passos:

A alternativa correta foi assinalada por 54,4% dos respondentes, sendo que no Grupo de Menor Desempenho o índice de acerto foi de pouco mais de 25%, ou seja, para cada 4 estudantes desse Grupo apenas 1 assinalou a opção correta. Além disso, nesse Grupo, a distribuição das alternativas foi muito próxima, o que sugere a possibilidade de uma escolha aleatória de respostas para a maioria desses alunos. Em contrapartida, no Grupo de Maior Desempenho o índice de acerto foi superior a 80%, indicando maior familiaridade com esse tipo de tarefa.
A Curva Característica do Item mostra que os alunos cuja proficiência pode ser classificada como Abaixo do Básico têm, no máximo, 50% de chance de responder corretamente essa tarefa, já àqueles atrelados ao nível Básico têm entre 50% e 90% de probabilidade de assinalar a alternativa correta, enquanto que os estudantes de níveis Adequado e Avançado têm mais de 90% de chance de resolver corretamente esse problema, porém, esse grupo corresponde a apenas 6,5% dos alunos da rede estadual.
É importante ressaltar que o problema proposto tem como facilitador o fato de o sistema que modela esse problema já estar detalhado no enunciado do problema, ou seja, não há a necessidade de o aluno ter que criar um sistema que o modele. Além disso, conforme citado anteriormente, o problema já traz um sistema escalonado e com apoio visual de esquema, que favorece a não utilização de linguagem e técnicas algébricas para obtenção da solução.
Frente a isso, é importante que o professorado esteja atento para a necessidade de aumentar o índice de acerto em casos como esse, esclarecendo possíveis dúvidas dos alunos com menores níveis de proficiência, além de fornecer novos problemas em que a modelagem não é apresentada no enunciado, fazendo com que o aluno tenha que compreender, modelar e resolver o problema. Ressalta ainda a maior complexidade dos problemas que envolvem valores não inteiros ou razões para modelagem do sistema linear. |
 |
Exemplo 3
Nível Adequado
Compõe a descrição do ponto 350 da Escala de Matemática – SARESP


O item está atrelado a habilidade H33 – Resolver problemas que envolvam probabilidade simples – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o tema probabilidade é tratado desde o Ensino Fundamental, sendo retomado no 3º bimestre da 2ª Série do Ensino Médio. A tarefa proposta no item remete a definição clássica de probabilidade, vista em ciclos anteriores ao Ensino Médio, que é a razão entre o número de casos favoráveis e o número total de casos possíveis.
Frente a isso, uma solução para esse problema seria a contagem do número de quadrinhos que possuem um triângulo desenhado (12) dividido pelo número total de quadrinhos presentes na figura (100). Consequentemente, a probabilidade pode ser dada pela fração . Um detalhe importante é que a alternativa correta não apresenta exatamente essa fração, mas sim uma fração equivalente a essa. Aqui, vale destacar que como se trata de uma simplificação, o numerador da fração reduzida terá que ser um divisor do número de triângulos, ou seja, um divisor de 12. Com isso, apenas as alternativas (D) e (E) poderia ser opções de resposta. Ao fazer a simplificação corretamente obtém-se , nesse caso, a fração reduzida (alternativa D) como sendo a probabilidade.
O item foi classificado com dificuldade média, sendo que para cada 20 respondentes apenas 7 assinalam a alternativa correta. A distribuição das respostas dadas pelos estudantes mostra que a alternativa (C) foi a mais escolhida nos Grupos de Menor de Desempenho e Intermediário, possivelmente por confundirem o comando e calcularem a probabilidade de apontar para o quadrinho que tinha um retângulo desenhado. As alternativas (A) e (B), juntas, foram assinaladas por pouco mais de 25% dos respondentes e referem-se a probabilidade de apontar para a estrela ou para o círculo, respectivamente. A alternativa (E), escolha de pouco mais de 11% dos estudantes não é a probabilidade de nenhuma das figuras no quadro, sendo obtida possivelmente por meio de cálculos incorretos.
A Curva Característica do Item mostra que alunos no nível Abaixo do Básico (quase 50% do público) tem probabilidade de acerto muito próxima a de um acerto casual, ou seja, apesar de estar atrelado a conceitos estudados no Ensino Fundamental, como probabilidade e fração equivalente, é necessário que o aluno demostre capacidade de mobilização conjunta desses conhecimentos para obtenção da resposta. Já aqueles cuja probabilidade é classificada no nível Básico, a chance de acerto parte de 30%, podendo chegar a 80% conforme sua proficiência aumenta. Somente para os estudantes no nível Adequado e Avançado a probabilidade de resolver corretamente essa tarefa é superior a 80%.
A seguir são detalhadas algumas variações e observações que podem ser propostas a fim de identificar qual o dificultador para a obtenção da resposta correta nesse tipo de problema.
- Apresentar todas as respostas utilizando frações com denominador 100 ou fornecer a respostas em porcentagem.
- com isso identifica-se a dificuldade na obtenção da fração equivalente.
- detalhe: perceberão os alunos que se trata da mesma resposta?
- Questionar se a resposta não deveria ser , afinal temos 4 tipos de figuras e o triângulo é apenas uma delas.
- a intenção é verificar se o estudante é capaz de atentar-se para o fato de como o número de cada tipo de figura é diferente, então esse pensamento não pode ser validado.
- E se as figuras não estivessem agrupadas, qual seria a probabilidade?
- desse modo é possível perceber a posição dos elementos como um invariante já que se trata de um sorteio aleatório.
- E se o evento tivesse que ocorrer repetidas vezes, como ficaria o cálculo da probabilidade?
- há várias possibilidades de estudo nesse caso, inclusive a de sortear o triângulo algumas e não todas as vezes.
duas questões da prova de 2019 avaliaram esse tipo de tarefa e o índice de acerto foi menor do que o observado para o item em discussão.
|
 |
Exemplo 4
Nível Avançado
Compõe a descrição do ponto 400 da Escala de Matemática – SARESP
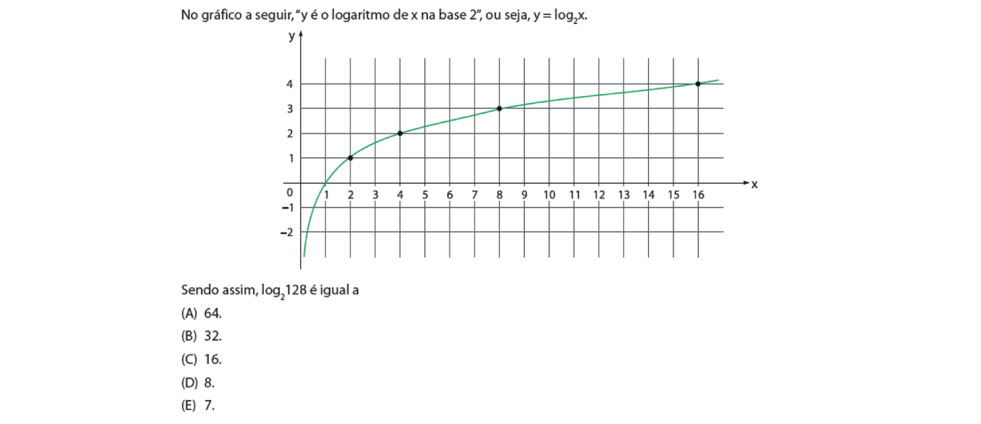

O item está atrelado a habilidade H11 – Aplicar o significado de logaritmos para a representação de números muito grandes ou muito pequenos, em diferentes contextos – segundo a Matriz de Referência de Avaliação do SARESP, sendo que o tema logaritmos é tratado no 3º bimestre da 1ª Série e o estudo gráfico de funções, inclusive a logarítmica, é visto no 3º bimestre da 3ª série do Ensino Médio. A tarefa proposta no item envolve a determinação do valor de log2 128, tendo como apoio a representação gráfica da função y = log2 x.
Para resolver o problema é necessário que o estudante associe o log2 128 com a potenciação de base 2, ou seja, o valor do log2 128 é o valor do expoente que se eleva o número 2 para obter 128. Nesse caso, log2 128 = 7 já que 27 = 128. Detalhe importante consiste em perceber que o gráfico tem como finalidades:
- informar o valor de alguns logaritmos na base 2, porém não se observa o valor de a partir de uma leitura direta do gráfico;
- o comportamento da curva mostra que não há proporção entre os valores de x e y apresentados no gráfico.
A partir do gráfico, a resposta pode ser obtida mediante uso da seguinte propriedade de logaritmos: log2 a . b = log2 a + log2 b. Assim, tem-se que:
log2 128 = log2 16 . 8 = log2 16 + log2 8 = 4 + 3 = 7 (alternativa A)
A alternativa correta foi assinalada por menos de 10% dos respondentes, o que mostra que 9 em cada 10 respondentes optam por uma alternativa incorreta. Mesmo no Grupo de Maior Desempenho o índice de acerto é de apenas 15,7%. Assim, o item é caracterizado como sendo muito difícil, apresentando uma discriminação fraca. A Curva Característica do Item reforça essas características do item ao mostrar que para alunos cuja proficiência é inferior a 300, a probabilidade de acerto é similar ao de um acerto casual. Detalhe importante é ressaltar que a média estadual é inferior a 300.
A partir da distribuição das respostas dos estudantes, percebe-se que mais da metade dos respondentes optaram pelas alternativas (A) ou (B), apesar de 264 e 232 serem números de ordens astronômicas. Certamente, os alunos que optaram por essas respostas não consideraram o pensamento exponencial em seu raciocínio, por exemplo, no caso do 64, é muito provável que os respondentes pensaram na divisão, calculando a metade de 128. Inclusive, cabe registrar que a opção pela alternativa (A) ocorreu em maior frequência pelos alunos do Grupo de Maior Desempenho.
Vale ressaltar que esse tipo de confusão foi detectado na prova do 7º Ano do Ensino Fundamental, quando a maior parte dos alunos indicou que 32 é igual a 6 e não a 9. Esse tipo de equívoco se não for devidamente trabalhado faz com que o alunado carregue esse tipo de erro conceitual para momentos futuros do seu estudo em matemática, como é caso do exemplo apresentado.
Por fim, é importante frisar que a análise do gráfico precisa levar em consideração que o pensamento exponencial apresenta um crescimento mais acentuado e rápido que a função afim. Do contrário, o estudante irá considerar que x = 128 é um valor muito distante de x =16 (último valor apresentado graficamente) e, consequentemente, y = log2 128 será um valor distante de log2 16 = 4. Reconhecer as particularidades e comportamentos das funções é uma das principais expectativas para essa temática no Ensino Médio.
|
|
|
|

|
