| A edição 2017 do SARESP aferiu a proficiência dos estudantes do 7º Ano do Ensino Fundamental, cuja média foi de 228,4. Esse valor é um pouco superior ao obtido na edição anterior da prova, de modo a classificar a proficiência desse conjunto de estudantes como de nível Básico. A distribuição dos alunos nos níveis de proficiência aponta 25,3% dos alunos no nível Abaixo do Básico, 44,5% no nível Básico, 25,9% no nível Adequado e apenas 4,3% no nível Avançado. A prova baseada nas habilidades da MRA SARESP, contemplando todas as habilidades da matriz, sendo que os percentuais mais baixos de acerto foram diagnosticados em itens referentes a identificar as diferentes representações de um número racional (fração, decimal e porcentagem), tanto em perguntas diretas como em situações-problema; além da resolução de problemas envolvendo a comparação entre diferentes unidades de medida (de tempo e de capacidade). Em contrapartida, notou-se um desempenho muito bom em resolver situações-problema envolvendo a soma entre números decimais, em contextos familiares aos estudantes; associar gráficos e tabelas, assim como fazer a leitura de diagramas de árvore para resolver problemas de combinatória. 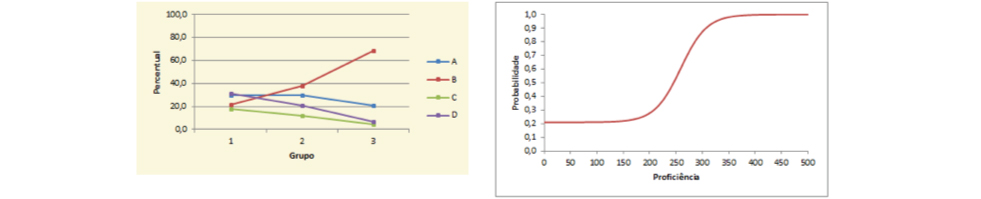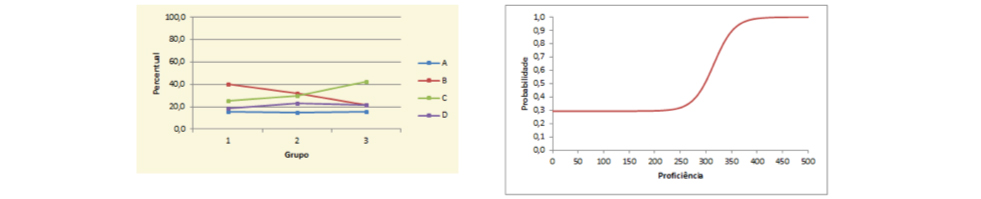Em seguida são apresentados exemplos comentados a fim de ilustrar atividades características que os alunos de cada nível de proficiência são capazes de realizar. Além do enunciado e a solução dos itens, há uma análise gráfica da frequência de escolha de cada alternativa nos três Grupos de Desempenho e a Curva Característica do Item que associa a proficiência do respondente e a probabilidade de acertar a questão. 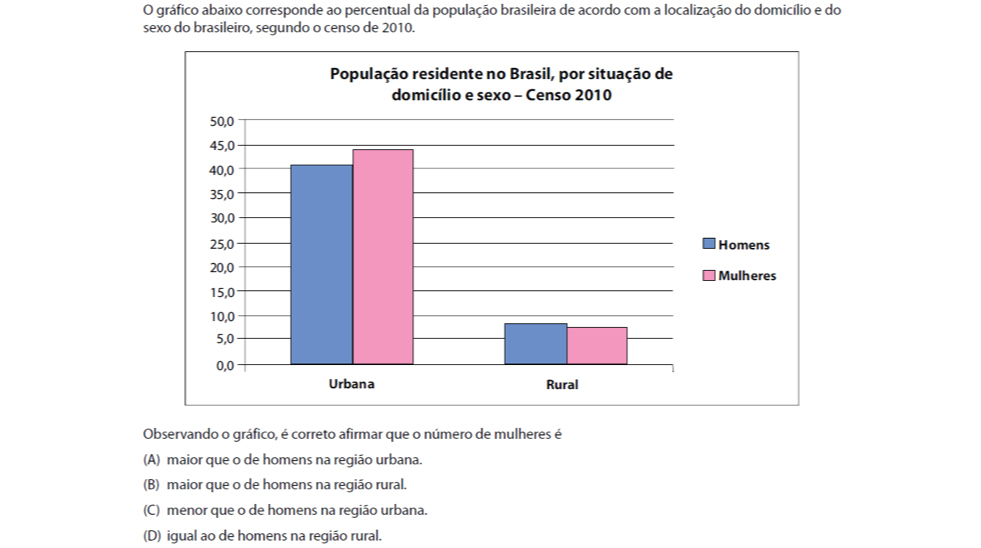Exemplo 1 Nível: Abaixo do básico Compõe a descrição do ponto 150 da Escala de Matemática – SARESP    O item apresentado propõe a análise de afirmações feitas a partir de um gráfico de colunas para identificar qual é a verdadeira. Essa tarefa está associada a habilidade H35 da MRA SARESP do 7ºEF, descrita como “Identificar e Interpretar informações transmitidas por meio de gráficos”. Essa habilidade está associada a diferentes expectativas, desde os anos iniciais do Ensino Fundamental, sendo novamente discutida no 4º bimestre do 6º Ano EF. Para resolvê-lo corretamente é necessário comparar o percentual de mulheres, em relação ao de homens, residentes na área urbana e rural por meio de um gráfico de colunas. A partir dessa comparação, é possível concluir que o número de mulheres é maior que o de homens na região urbana, haja vista que a altura da coluna das mulheres é maior que a dos homens nesse tipo de área, o que faz a alternativa (A) ser verdadeira. 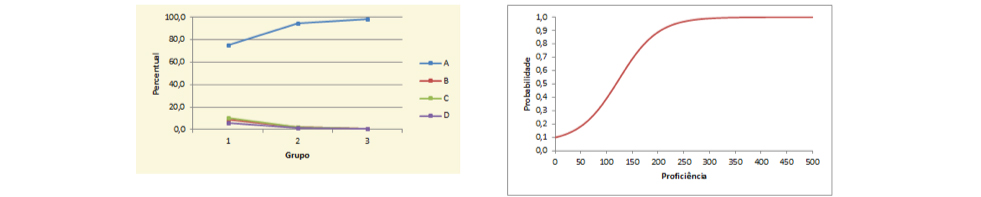O item foi acertado por aproximadamente 90% dos respondentes, o que o faz ser classificado como um item muito fácil. Mesmo no Grupo de Menor Desempenho, mais de ¾ dos estudantes realizaram corretamente essa tarefa. A Curva Característica do Item reforça a expectativa de bom desempenho, uma vez que mesmo alunos cujas proficiências estão classificadas no nível Abaixo do Básico, porém próximos da fronteira com o nível Básico, têm em torno de 80% de probabilidade de acertar essa questão. Sugere-se ao professorado que explore as diversas possibilidades que o gráfico permite, inclusive apresentando questionamentos com maior grau de complexidade, como, por exemplo:
|
 |
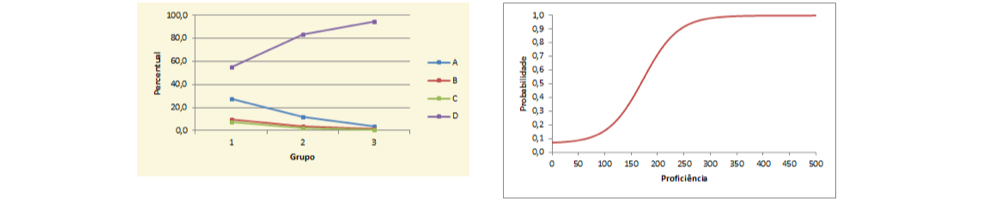
| Exemplo 2 Nível Básico Compõe a descrição do ponto 200 da Escala de Matemática – SARESP    O item proposto compara a probabilidade de sortear um prêmio entre as crianças, homens e mulheres presentes em uma festa, sendo fornecido o número de crianças, homens e mulheres que estavam na festa. Essa tarefa está associada a habilidade H33 da MRA SARESP do 7º Ano EF, descrita como “Resolver problemas que envolvam probabilidade de eventos simples”. Expectativas de aprendizagem associadas a probabilidade aparecem no 4º e 5º anos do Ensino Fundamental e novamente no 3º bimestre do 7º ano Ensino Fundamental. Para resolver corretamente a questão é necessário saber calcular a probabilidade de sortear uma pessoa, sendo ela criança, homem ou mulher. Dado que ao todo há 70 pessoas nessa festa, sendo 20 crianças, 25 homens e 25 mulheres, tem-se:  Consequentemente, a alternativa (A) é falsa já que a probabilidade de sortear uma criança implica na menor das três frações. As alternativas (B) e (C) também são incorretas uma vez que não há uma fração que seja maior que as demais. Ao comparar as três frações, conclui-se que a alternativa (D) é a correta, já que a probabilidade de um homem ser sorteado, assim como a de uma mulher ser sorteada, é igual a 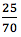 .É importante que o estudante perceba que, individualmente, todos os convidados da festa, seja criança, homem ou mulher, têm a mesma chance 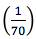 de ser sorteado. No entanto, isso não é justificativa para afirmar que crianças, homens e mulheres possuem a mesma probabilidade de serem sorteados, visto que ao considerar a probabilidade de sortear qualquer convidado do grupo de crianças ou do grupo de homens ou do grupo de mulheres, é preciso considerar o número de pessoas em cada grupo. Logo, a probabilidade será maior naquele grupo que contém maior número de integrantes.A Curva Característica do Item mostra que alunos cuja proficiência está associada ao nível Abaixo do Básico tem probabilidade inferior a 75% de acertar essa questão, enquanto que alunos de nível Básico têm probabilidade igual ou superior a 75%, podendo chegar a quase 98% no caso dos alunos de nível Adequado de proficiência. Já os de nível avançado tem probabilidade muito próxima a 100% de responder corretamente esse item. O problema em questão foi acertado por quase 80% dos respondentes, sendo que a alternativa correta foi a mais escolhidas nos três Grupos de Desempenho. É de extrema importância que as motivações que levaram os demais a escolher outra alternativa como resposta sejam investigadas na sala de aula. O esclarecimento do equívoco visa evitar que ideias incorretas continuem sendo tidas como justificativas válidas para os estudantes. Muitas vezes, os estudantes apoiam suas decisões em argumentos não baseados na probabilidade. Para inverter esse cenário é preciso propor diversas situações em que a problemática proposta seja plausível para a turma, de modo a permitir que o estudante a explore, o professor possa questioná-lo, buscando construir novas ideias que valorizem o conhecimento formal. Ao analisar outras tarefas associadas à habilidade em questão, percebe-se que os alunos apresentam maior dificuldade em calcular a probabilidade de um evento que apresenta duas características. Por exemplo, em uma urna com 50 bolas coloridas e enumeradas, a probabilidade de sortear uma bola com determinado tipo de número e certa cor é, para um contingente considerável de respondentes, igual a 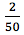 . É importante verificar se a justificativa da utilização do número 2 está pautada no fato da bola desejada ter duas características.
Também é fundamental mostrar para os alunos que o aumento das condições daquilo que se quer sortear não implica no aumento da probabilidade de isso ocorrer. A própria sala de aula pode servir como prova para tanto. Por exemplo, é mais provável sortear um menino, loiro e que usa óculos ou simplesmente um menino (sem condicionar outras características)? |
|
| Exemplo 3 Nível Adequado Compõe a descrição do ponto 275 da Escala de Matemática – SARESP    O item apresentado propõe uma situação-problema de um jogo, no qual o participante sorteia duas fichas e soma os valores presentes nas fichas. Na situação proposta deve-se somar um número negativo e um número positivo. Essa tarefa está associada a habilidade H03 da MRA SARESP do 7º Ano EF, descrito como “Resolver problemas que envolvam as quatro operações básicas entre números inteiros”. O conjunto dos números inteiros é um tema cujo trabalho é iniciado especificamente no 7º Ano EF, sem estar ligado a expectativas de anos anteriores. Para resolver corretamente o problema, é necessário compreender que a tarefa é calcular a soma entre os dois números apresentados, ou seja, efetuar (–27) + (+14). Ao somar números positivos com números negativos, é necessário atentar-se a diferença entre os números, mantendo o sinal daquele que é maior em módulo. De maneira mais simplificada, ocorre que o (+14), ou seja, as 14 unidades positivas anulam 14 das 27 unidades negativas (–27), o que implica na sobra de 13 unidades negativas, ou seja, a resposta para o problema é (–13), alternativa (B). O item foi respondido corretamente por 43,3% dos estudantes, sendo a alternativa com maior frequência de resposta no Grupo de Desempenho Intermediário, mas principalmente no Grupo de Maior Desempenho, o que garante ao item um índice de discriminação muito bom, segundo a TCT. As alternativas (A) e (D), juntas, atraíram pouco mais de 45% dos respondentes, apresentando, respectivamente, –41 e +41 como opções de resposta. Nesse caso, a opção pela resposta 41, negativo ou positivo, provavelmente é motivada por 41 ser a soma dos números 27 e 14. Ou seja, os respondentes realizaram a soma dos números, ignorando seus sinais, e aplicaram incorretamente alguma regra para decidir se o resultado seria positivo ou negativo. Ressalta-se que essa forma de calcular, operando os números primeiro para então definir o sinal do resultado é característico das operações multiplicação e divisão envolvendo números inteiros. A Curva Característica do Item mostra que alunos com nível de proficiência Abaixo do Básico têm probabilidade de acerto muito próxima a de um acerto casual. Já alunos de nível Básico de proficiência podem chegar a ter, aproximadamente, 50% de responder corretamente essa tarefa. Apenas alunos nos níveis Adequado e Avançado apresentam maior chance de acerto do que erro, sendo que os alunos do nível Avançado têm probabilidade de acerto superior a 85%. Explorar diferentes cálculos entre números inteiros é fundamental para o aprimoramento da técnica de cálculo. Afinal, tanto a soma como a subtração entre números inteiros podem apresentar como resultado números positivos, negativos ou, até mesmo, zero. Também é importante ter claro que há particularidades ao efetuar uma multiplicação ou divisão no conjunto dos números inteiros, que não são válidas no cálculo de uma adição ou subtração e vice-versa. Além disso, há um complicador. Os símbolos utilizados para representar os números positivos e negativos são os mesmos utilizados para representar as operações de soma e subtração. Saber distinguir quando os símbolos se referem a uma característica do número ou a uma operação é fundamental para que toda a aritmética dos números inteiros seja plausível para o estudante. Daí a importância de carregar os parênteses durante os cálculos para restringir o sinal ( + ) aos números positivos e o sinal ( – ) aos números negativos. Muitas vezes o próprio professorado passa a suprimir essa simbologia e passa cometer abusos na escrita, o que de certa forma faz sentido para ele, assim como para alguns alunos, mas que contribui para que o estudo dos números inteiros passe a ser um tanto nebuloso. A análise de outros itens presentes na prova, associados a temática indicam uma dificuldade em interpretar os significados de números negativos e positivos na resolução de problemas, assim como na execução de cálculos envolvendo soma e subtração nesse conjunto numérico. |
|
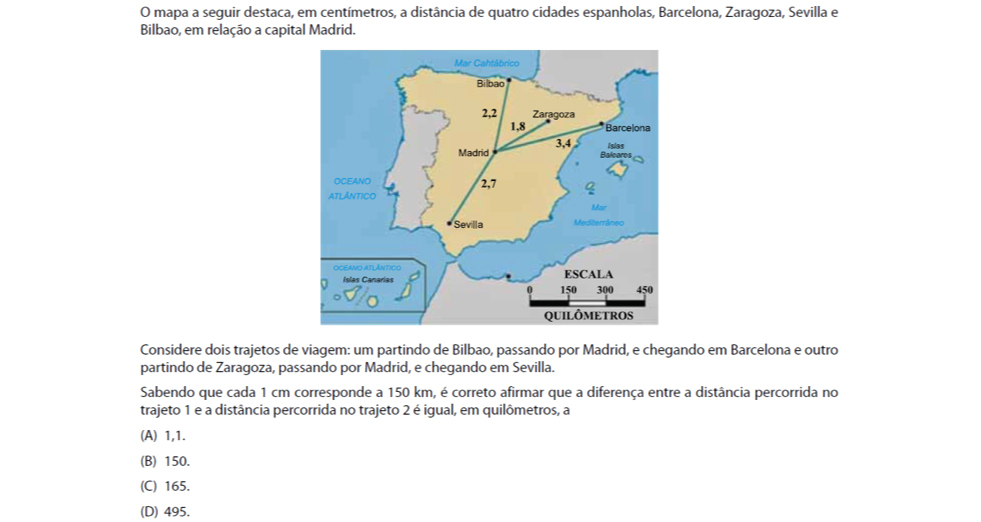
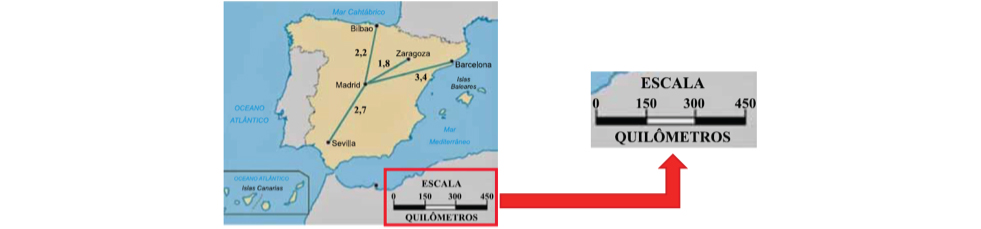
| Exemplo 4: Nível Avançado Compõe a descrição do ponto 325 da Escala de Matemática – SARESP    O problema apresenta um mapa, no qual tem-se a distância, em centímetros, entre cidades cujos nomes são indicados no mapa, de modo a obter a diferença entre a distância total percorrida, em quilômetros, de dois trajetos, fazendo uso da escala do mapa, descrita também textualmente. O item está associado a habilidade H32 da MRA SARESP do 7º Ano EF, descrita como “Usar desenhos de escalas para resolver problemas do cotidiano que incluam distância (como leitura de mapas)”. O estudo de escalas está contido numa expectativa de aprendizagem associada ao conceito de razão proposto no 3º bimestre do 7º Ano do Ensino Fundamental. Para resolver o problema corretamente é necessário, primeiramente, calcular a distância total dos dois trajetos, utilizando as informações presentes no mapa. O trajeto de Bilbao a Barcelona é constituído de uma primeira parte de 2,2 cm até Madrid e mais 3,4 cm para chegar ao destino final, totalizando 5,6 cm. O outro trajeto, de Zaragoza a Sevilla possui, 1,8 cm iniciais e mais 2,7 cm, totalizando 4,5 cm. Ou seja, a diferença entre as distâncias, baseado no mapa, é de 1,1 cm. Provavelmente foi essa conclusão que motivou pouco mais de 15% dos alunos a optar pelo distrator (A). Dado, tanto no mapa como textualmente, que cada 1 cm corresponde a 150 km, então a diferença real entre as distâncias percorridas é igual o produto entre 1,1 e 150, que resulta em 165 km, ou seja, a alternativa (C), assinalada por pouco menos de um terço dos alunos que responderam essa questão. O distrator (B) foi quase tão escolhido quanto a alternativa correta, sendo que a motivação para tanto pode se dar pelo fato do 150 estar destacado no enunciado da questão ou então por um erro de cálculo ao apontar que a diferença de distância entre os trajetos, no mapa, era igual a 1 cm. O último distrator, alternativa (D), apresenta um valor que é o triplo da distância correta, mas cuja obtenção é fruto de uma sequência de cálculos e leitura do texto equivocados. É importante verificar se os alunos seriam capazes de resolver a questão sem a informação textual de “cada 1 cm corresponde a 150 km”, ou seja, baseado na leitura correta da escala presente no canto inferior direito do mapa.  Para ampliar os conhecimentos frente a esse tipo de tarefa, recomenda-se explorar outros possíveis trajetos nesse mapa, ou então abordar diferentes tipos de mapas, ou até mesmo um determinado local apresentado em mapas com diferentes escalas. Aliás, o que aconteceria com as distâncias indicadas, em centímetros, no mapa se a escala fosse 1:300? E qual seria a nova escala se a distância entre as cidades indicadas triplicasse? Seria essa relação entre as distâncias proporcional? Direta ou inversamente? A Curva Característica do Item mostra que para alunos cuja proficiência é inferior a 250, apresenta uma probabilidade de acerto muito próxima a de um acerto casual, o que mostra que mesmo para alunos de nível Adequado, resolver corretamente esse problema não se mostra tão simples. A probabilidade de acerto passa a ser superiora a 70% somente para estudantes com proficiência igual ou superior a 325. |